$Q1$.
$2$ つのベクトル $\overrightarrow{a} = (6,-3)$, $\overrightarrow{b} = (-8t + 4, 2t-10)$ が平行になるように実数 $t$ の値を定めなさい。

$Q1$.
$|\overrightarrow{a}| = 1$, $|\overrightarrow{b}| = 2$ かつ, $\overrightarrow{a}$ と $\overrightarrow{b}$ のなす角 $\theta$ が $\dfrac{\pi}{3}$ の時, $\overrightarrow{a}$ と $\overrightarrow{b}$ の内積を求めなさい。

$Q1$.
$\overrightarrow{a} = (-2,-5)$, $\overrightarrow{b} =(3,-3)$ に対し $-3\overrightarrow{a} + \overrightarrow{b}$ の成分表示とその大きさを求めなさい。

$Q1$.
正六角形 ${\rm ABCDEF}$ において $\overrightarrow{a} = \overrightarrow{{\rm AF}}$, $\overrightarrow{b} = \overrightarrow{{\rm AB}}$ とする。

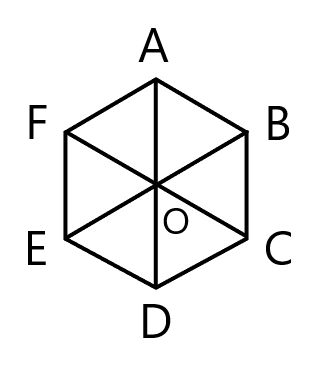
この時, 次のベクトルを $\overrightarrow{a}$, $\overrightarrow{b}$ を用いて表しなさい。

$Q1$.
正方形 ${\rm ABCD}$ の頂点を始点と終点に持つベクトルを考える。

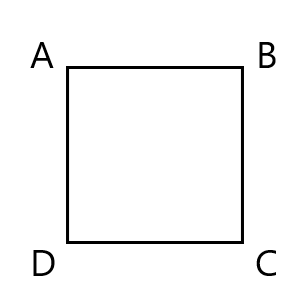
この時, 以下の問いに答えなさい。