$Q1$.
正六角形 ${\rm ABCDEF}$ において $\overrightarrow{a} = \overrightarrow{{\rm AF}}$, $\overrightarrow{b} = \overrightarrow{{\rm AB}}$ とする。
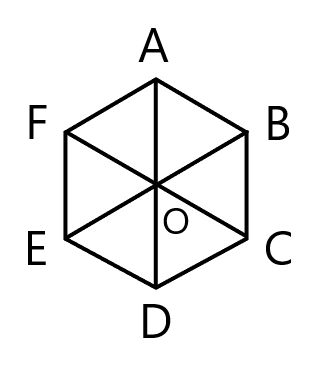
この時, 次のベクトルを $\overrightarrow{a}$, $\overrightarrow{b}$ を用いて表しなさい。
$Q2$.
次のベクトルを整理しなさい。
括弧を外し, $\overrightarrow{a}$, $\overrightarrow{b}$ のそれぞれの係数をまとめましょう。
(1)
$\begin{eqnarray*} \left( 2\overrightarrow{a} + 4\overrightarrow{b} \right) + \left( -\overrightarrow{a} -2\overrightarrow{b}\right) & = & 2\overrightarrow{a} - \overrightarrow{a} + 4\overrightarrow{b} - 2\overrightarrow{b}\\[0.5em] & = & (2-1)\overrightarrow{a} + (4-2)\overrightarrow{b} \\[0.5em] & = & \overrightarrow{a} + 2\overrightarrow{b} \end{eqnarray*}$
(2)
数の計算の時と同様に, 分配法則が成り立ちます。
$\begin{eqnarray*} 2\left(-2\overrightarrow{a} + 2\overrightarrow{b} \right) + 4\left( 2\overrightarrow{a} +4\overrightarrow{b}\right) & = & -4\overrightarrow{a}+4\overrightarrow{b} + 8\overrightarrow{a} + 16\overrightarrow{b} \\[0.5em] & = & (-4+8)\overrightarrow{a} +(4+16)\overrightarrow{b}\\[0.5em] &= & 4\overrightarrow{a} + 20\overrightarrow{b} \end{eqnarray*}$
$Q3$.
次の式が成り立つ時, $\overrightarrow{x}$ を $\overrightarrow{a}$, $\overrightarrow{b}$ を用いて表しなさい。
$\overrightarrow{x}$ を左辺に, それ以外のベクトルを右辺に移項します。
$\begin{eqnarray*} -4\overrightarrow{x} + 3\overrightarrow{x} & = & 3\overrightarrow{a} + \overrightarrow{b} -2\overrightarrow{a} + \overrightarrow{b}\\[0.5em] -\overrightarrow{x} & = & \overrightarrow{a} + 2\overrightarrow{b}\end{eqnarray*}$
両辺に $-1$ をかければ
$\overrightarrow{x} = -\overrightarrow{a} -2\overrightarrow{b}$
となります。
$Q4$.
次の $2$ つの式が成り立つ時, $\overrightarrow{x}$, $\overrightarrow{y}$ を $\overrightarrow{a}$, $\overrightarrow{b}$ を用いて表しなさい。
連立方程式を解く時と同じ要領で解いていきましょう。
$\begin{eqnarray*} -\overrightarrow{x} + 2\overrightarrow{y} & = & -4\overrightarrow{a}~~\cdots (1)\\[0.5em] -\overrightarrow{x} + 4\overrightarrow{y} & = & -4\overrightarrow{b}~~\cdots (2)\end{eqnarray*}$
とすると, $(2) - (1)$ より
$2\overrightarrow{y} = 4\overrightarrow{a} -4\overrightarrow{b}$
両辺を $2$ で割れば
$\overrightarrow{y} = 2\overrightarrow{a} - 2\overrightarrow{b}$
これを $(1)$ に代入して整理すると
$\begin{eqnarray*} \overrightarrow{x} & = & 2\overrightarrow{y} + 4\overrightarrow{a}\\[0.5em] & = & 2\left( 2\overrightarrow{a} - 2\overrightarrow{b} \right) + 4\overrightarrow{a}\\[0.5em] & = & 8\overrightarrow{a} - 4\overrightarrow{b}\end{eqnarray*}$

(1)
$\overrightarrow{{\rm BE}} = 2\overrightarrow{{\rm AF}}$
なので $\overrightarrow{{\rm AF}} = 2\overrightarrow{a}$ となります。
(2)
$\overrightarrow{{\rm AO}}=\overrightarrow{{\rm AF}} + \overrightarrow{{\rm FO}}=\overrightarrow{{\rm AF}} + \overrightarrow{{\rm AB}}$
なので $\overrightarrow{{\rm AO}} = \overrightarrow{a}+ \overrightarrow{b}$ となります。
(3)
$\overrightarrow{{\rm AE}} = \overrightarrow{{\rm AF}} + \overrightarrow{{\rm FE}} = \overrightarrow{{\rm AF}} + \overrightarrow{{\rm AO}}$
であり, $\overrightarrow{{\rm AO}} = \overrightarrow{a} + \overrightarrow{b}$ であるから
$\overrightarrow{{\rm AE}} = \overrightarrow{a} + \left( \overrightarrow{a} + \overrightarrow{b} \right) = 2\overrightarrow{a} + \overrightarrow{b}$
となります。
(4)
$\overrightarrow{{\rm CO}} = \overrightarrow{{\rm BA}} = -\overrightarrow{{\rm AB}}$
より $\overrightarrow{{\rm CO}} = -\overrightarrow{b}$ となります。
(5)
$\overrightarrow{{\rm AD}} = 2\overrightarrow{{\rm AO}}$
より $\overrightarrow{{\rm AD}} = 2\overrightarrow{a}+2\overrightarrow{b}$ となります。
(6)
$\overrightarrow{{\rm FB}} = \overrightarrow{{\rm FA}} + \overrightarrow{{\rm AB}} = -\overrightarrow{{\rm AF}} + \overrightarrow{{\rm AB}}$
より $\overrightarrow{{\rm FB}} = - \overrightarrow{a} + \overrightarrow{b}$ となります。