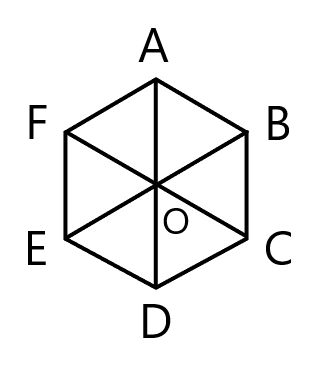
正六角形 ${\rm ABCDEF}$ において, $2\overrightarrow{{\rm AB}}$ と等しいベクトルを以下の選択肢から選びなさい。
$\overrightarrow{{\rm FC}}$
$\overrightarrow{{\rm AB}}$
$\overrightarrow{{\rm DE}}$
$\overrightarrow{{\rm AD}}$
${\rm ABCDEF}$ は正六角形であるから $\overrightarrow{{\rm AB}}$ と向きが同じで長さが $2$ 倍であるベクトルは $\overrightarrow{{\rm FC}}$ である。
正六角形 ${\rm ABCDEF}$ において, $-\overrightarrow{{\rm AF}}$ と等しいベクトルを以下の選択肢から選びなさい。

$\overrightarrow{{\rm DC}}$
$\overrightarrow{{\rm CD}}$
$\overrightarrow{{\rm EB}}$
$\overrightarrow{{\rm OO}}$
$\overrightarrow{{\rm AF}}$ と長さが等しく向きが反対であるベクトルは $\overrightarrow{{\rm DC}}$ である。
一般に $(-1)$ 倍されたベクトルは元のベクトルの逆ベクトルになる。
$(-1)\overrightarrow{a} = -\overrightarrow{a}$
正六角形 ${\rm ABCDEF}$ において, $0\overrightarrow{{\rm AD}}$ と等しいベクトルを以下の選択肢から選びなさい。

$\overrightarrow{{\rm AA}}$
$\overrightarrow{{\rm AO}}$
$\overrightarrow{{\rm AD}}$
$\overrightarrow{{\rm DA}}$
一般にベクトルを $0$ 倍したものは零ベクトルになる。
$0\overrightarrow{a} = \overrightarrow{0}$
よって $0 \overrightarrow{{\rm AD}} = \overrightarrow{{\rm AA}}$ である。
正六角形 ${\rm ABCDEF}$ において, $\dfrac{1}{2} \overrightarrow{{\rm CF}}$ と等しいベクトルを以下の選択肢から選びなさい。

$\overrightarrow{{\rm BA}}$
$\overrightarrow{{\rm ED}}$
$\overrightarrow{{\rm FC}}$
$\overrightarrow{{\rm CC}}$
${\rm ABCDEF}$ は正六角形であるから $\overrightarrow{{\rm CF}}$ と向きが同じで長さが $\dfrac{1}{2}$ 倍であるベクトルは $\overrightarrow{{\rm BA}}$ である。
正六角形 ${\rm ABCDEF}$ において, $-\dfrac{1}{2}\overrightarrow{{\rm BE}}$ と等しいベクトルを以下の選択肢から選びなさい。

$\overrightarrow{{\rm DC}}$
$\overrightarrow{{\rm AF}}$
$\overrightarrow{{\rm BE}}$
$\overrightarrow{{\rm EB}}$
${\rm ABCDEF}$ は正六角形であるから $\overrightarrow{{\rm BE}}$ と向きが反対で長さが $\dfrac{1}{2}$ 倍であるベクトルは $\overrightarrow{{\rm DC}}$ である。
