区間 $\alpha \lt t \lt \beta$ で $f'(t)$ の符号が一定の時, 媒介変数表示された曲線

$\left\{ $$\begin{aligned} x & = f(t) \\ y & =g(t) \end{aligned}$$ \right.$

と $x$ 軸, 直線 $x = f(\alpha)$, $x=f(\beta)$ で囲まれた図形の面積は

$\displaystyle S = \int_{\alpha}^{\beta} \left| g(t)f'(t) \right|~dt$

で計算することができます。

$y=0$ とすると $t=0,1$ なので, 求める面積 $S$ は

$ $$\begin{eqnarray*} S &=& \int_{0}^{1} \left|y\dfrac{dx}{dt} \right|\ dt \\[1em] &=& \int_{0}^{1} |t(1-t)\cdot 2t|\ dt \\[1em] &=& \int_{0}^{1} (2t^2-2t^3) \ dt \\[1em] &=& \left[\cfrac{2}{3} t^3-\dfrac{1}{2} t^4 \right]_0^1 = \cfrac{1}{6} \end{eqnarray*}$$ $

$y=0$ とすると $t=-1,2$ であり, $\dfrac{dx}{dt} = 2t$ より

$-1 \lt t \lt 0$ の時 $\dfrac{dx}{dt} \lt 0$, $~~0 \lt t \lt 2$ の時 $\dfrac{dx}{dt} \gt 0$

となります。

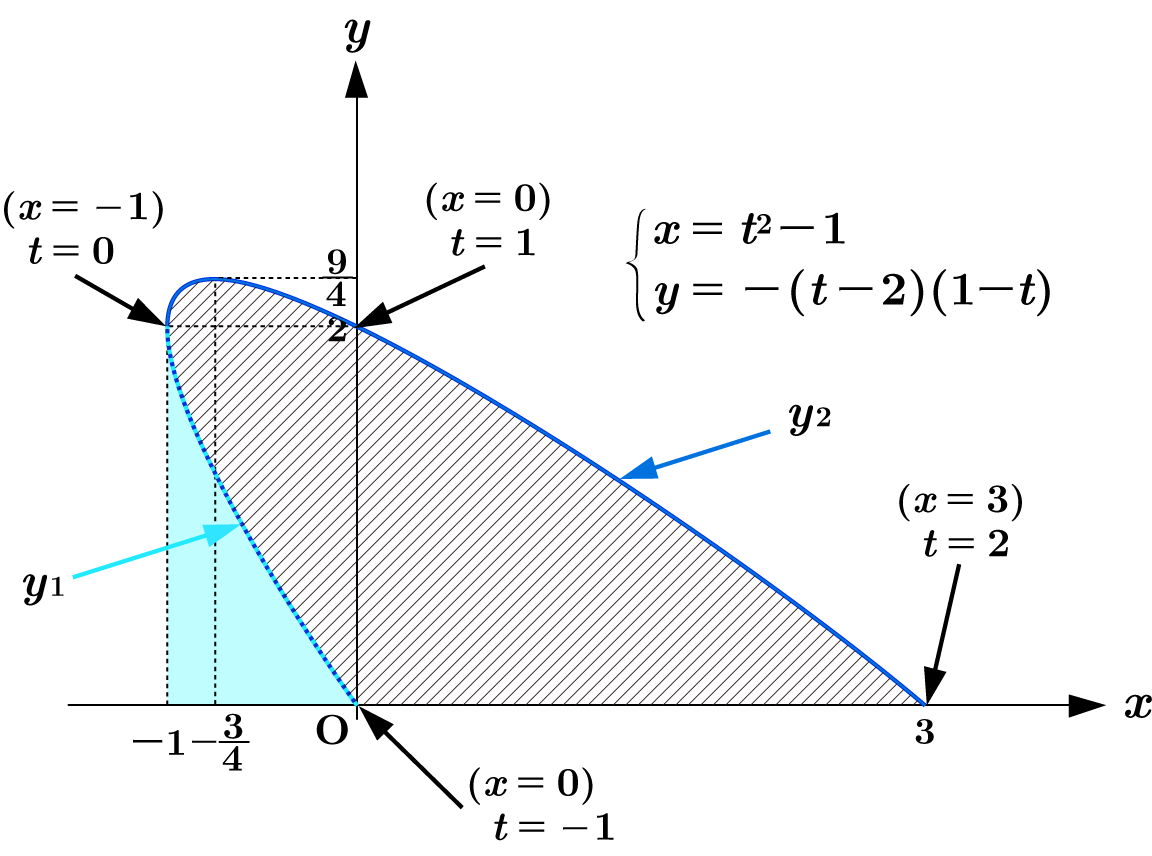
よって求める面積 $S$ は

$ $$\begin{eqnarray*} S&=&\int_{0}^{2} \left| y\cfrac{dx}{dt} \right|\ dt-\int_{-1}^{0} \left| y\cfrac{dx}{dt} \right|\ dt\\[1em] &=&\int_{0}^{2} |-(t-2)(t+1)2t|\ dt - \int_{-1}^{0} |-(t-2)(t+1)2t|\ dt\\[1em] &=&\int_{0}^{2} -(t-2)(t+1)2t\ dt - \int_{-1}^{0} (t-2)(t+1)2t\ dt\\[1em] &=&\int_{-1}^{2} -(t-2)(t+1)2t\ dt\\[1em] &=&\int_{-1}^{2} (-2t^3 + 2t^2 + 4t)\ dt\\[1em] &=&\left[-\cfrac{1}{2} t^4+\cfrac{2}{3} t^3+2t^2 \right]_{-1}^2 \\[1em] &=&\left(-8+\cfrac{16}{3}+8\right)-\left(-\cfrac{1}{2}-\cfrac{2}{3}+2\right) = \cfrac{9}{2} \end{eqnarray*}$$ $

この曲線を図示すると下のようになります。

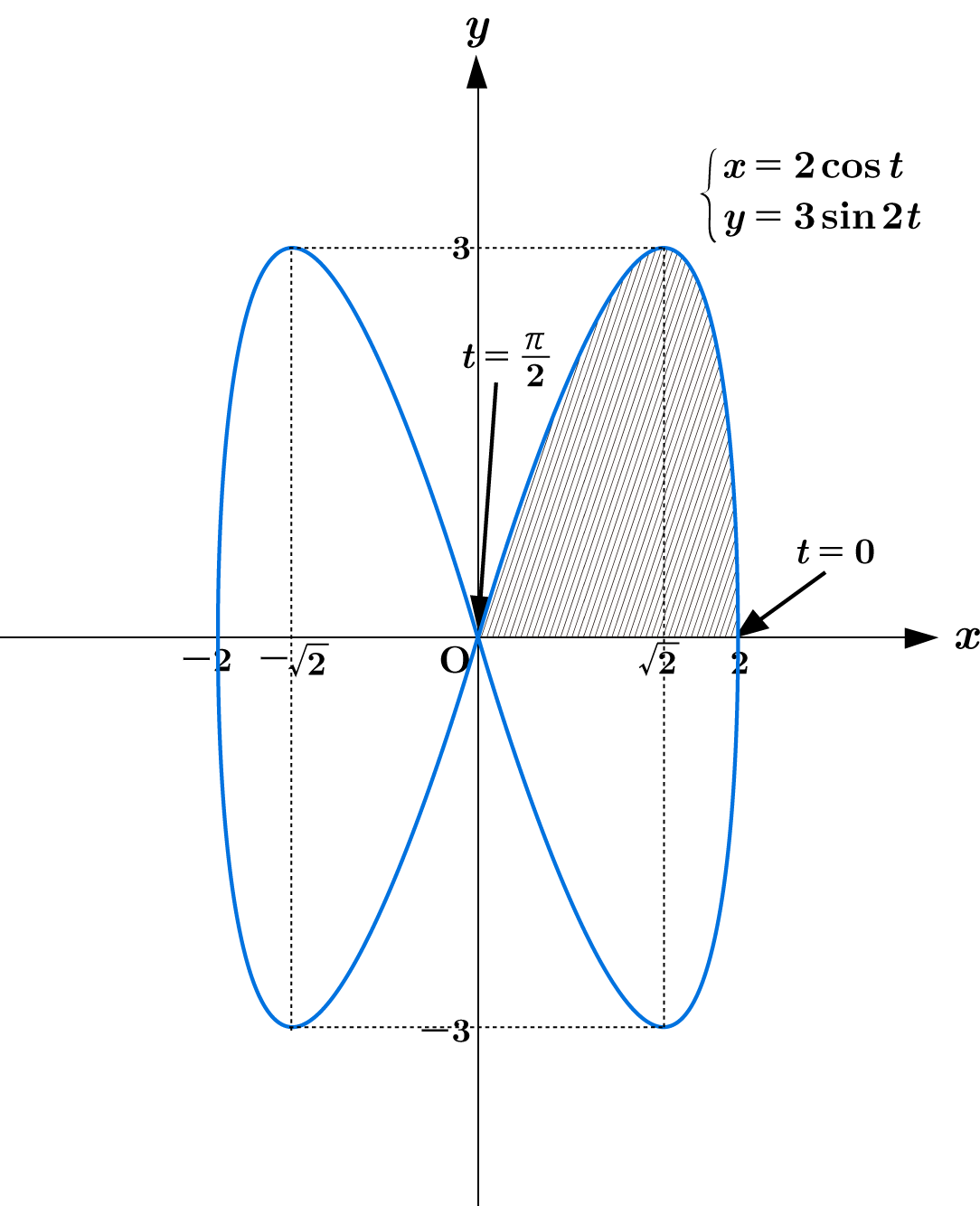
よって求める面積 $S$ は, 曲線の $0 \leqq t\leqq \dfrac{\pi}{2}$ における部分と $x$ 軸に囲まれた図形 (斜線部分) の面積の $4$ 倍になるので

$ $$\begin{eqnarray*} S&=& 4 \int_{0}^{\frac{\pi}{2}} \left| y \cfrac{dx}{dt} \right|\ dt\\[1em] &=& 4 \int_{0}^{\frac{\pi}{2}} \left| 3\sin 2t (-2\sin t) \right| \ dt\\[1em] &=& 24 \int_{0}^{\frac{\pi}{2}} \sin 2t \sin t \ dt\\[1em] &=& 24 \int_{0}^{\frac{\pi}{2}} (2\sin t \cos t) \sin t \ dt\\[1em] &=& 48 \int_{0}^{\frac{\pi}{2}} \sin^2 t \cos t \ dt = 48 \left[ \frac{1}{3}\sin^3 t \right]_{0}^{\frac{\pi}{2}} = 16 \end{eqnarray*}$$ $

媒介変数表示された曲線

$\left\{ $$\begin{aligned} x & = f(t) \\ y & =g(t) \end{aligned}$$ \right.~~(\alpha \leqq t \leqq \beta)$

の長さ $L$ は

$\displaystyle L = \int_{\alpha}^{\beta} \sqrt{ \left\{ f'(t) \right\}^2 + \left\{ g'(t) \right\}^2 }~dt = \int_{\alpha}^{\beta} \sqrt{ \left( \dfrac{dx}{dt} \right)^2 + \left( \dfrac{dy}{dt} \right)^2 }~dt$

で計算することができます。

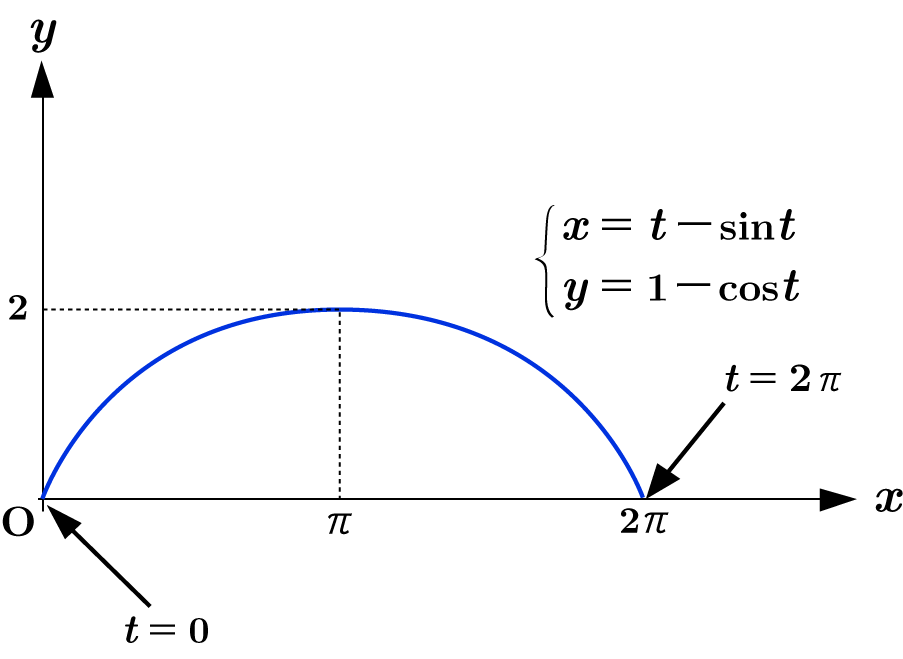
この式に当てはめて計算すると

$ $$\begin{eqnarray*} L &=&\int_{0}^{2\pi} \sqrt{(1-\cos t)^2+\sin^2 t } \ dt \\[1em] &=&\int_{0}^{2\pi} \sqrt{1-2\cos t+\cos ^2 t+\sin ^2 t} \ dt \\[1em] &=&\int_{0}^{2\pi} \sqrt{2-2\cos t} \ dt \end{eqnarray*}$$ $

半角の公式から

$1-\cos t = 2\sin^2 \dfrac{t}{2}$

であり, $0\leqq t \leqq 2\pi$ では $\sin \dfrac{t}{2} \geqq 0$ であることに注意すると

$ $$\begin{eqnarray*} L &=&\int_{0}^{2\pi} \sqrt{2-2\cos t} \ dt \\[1em] &=&\int_{0}^{2\pi} \sqrt{4\sin ^2 \cfrac{t}{2}} \ dt\\[1em] &=&\int_{0}^{2\pi} 2\sin \cfrac{t}{2} \ dt = 2\left[-2\cos \cfrac{t}{2}\right]_0^{2\pi} = 8 \end{eqnarray*}$$ $

※ この曲線は サイクロイドと呼ばれます。

媒介変数表示された曲線

$\left\{ $$\begin{aligned} x & = f(t) \\ y & =g(t) \end{aligned}$$ \right.$

と $x$ 軸, $x=f(\alpha)$, $x = f(\beta)~(\alpha \lt \beta)$ で囲まれた部分を $x$ 軸のまわりに回転してできる立体の体積 $V$ は

$\displaystyle V = \pi \int_{\alpha}^{\beta} \left\{ g(t) \right\}^2 \left| f'(t) \right|~dt$

で計算することができます。

計算すると

$ $$\begin{eqnarray*} V&=&\pi \int_{0}^{1} y^2 \left| \dfrac{dx}{dt} \right|\ dt \\[1em] &=& \pi \int_{0}^{1} t^2 (1-t)^2 2t\ dt \\[1em] &=& \pi \int_{0}^{1}(2t^3-4t^4+2t^5) \ dt \\[1em] &=& \pi \left[\cfrac{1}{2} t^4-\cfrac{4}{5} t^5+\cfrac{1}{3} t^6 \right]_0^1 \\[1em] &=& \left(\cfrac{1}{2}-\cfrac{4}{5}+\cfrac{1}{3}\right)\pi = \cfrac{\pi}{30} \end{eqnarray*}$$ $

曲線は上図のようになるので, 求める体積 $V$ は $0 \leqq t \leqq \dfrac{t}{2}$ に対応する部分を回転してできる立体の体積の $2$ 倍になります。よって

$ $$\begin{eqnarray*} V &=& 2 \int_{0}^{\frac{\pi }{2}} \pi y^2 \left| \cfrac{dx}{dt} \right|\ dt \\[1em] &=& 2 \pi \int_{0}^{\frac{\pi }{2}} 9\sin ^2 2t \ |-2\sin t|\ dt \\[1em] &=& 36\pi \int_{0}^{\frac{\pi }{2}} (2\sin t \cos t)^2\sin t \ dt\\[1em] &=& 144\pi \int_{0}^{\frac{\pi }{2}} \sin ^3 t\ \cos^2 t\ dt\\[1em] &=& 144\pi \int_{0}^{\frac{\pi }{2}} \sin t (1-\cos^2 t) \cos^2 t\ dt\\[1em] &=& 144\pi \int_{0}^{\frac{\pi }{2}} (\sin t \cos^2 t - \sin t \cos^4 t)\ dt\\[1em] &=& 144\pi \left[ -\dfrac{1}{3}\cos^3 t + \dfrac{1}{5}\cos^5 t \right]_0^{\frac{\pi}{2}}\\[1em] &=& 144 \pi \left( \cfrac{1}{3}-\cfrac{1}{5} \right)=\cfrac{96}{5}\pi \end{eqnarray*}$$ $