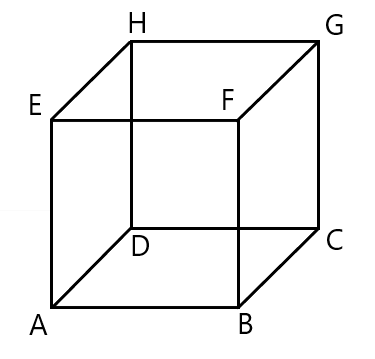
空間ベクトルの大きさ2 12345 : 現在の問題 : 前回正解 : 前回不正解 : 未挑戦 ※ このコンテンツはプレミアム会員限定です。問題 以下の立方体 ${\rm ABCDEFGH}$ において, $|\overrightarrow{{\rm AB}}|=1$ の時, $\overrightarrow{{\rm AH}}$ の大きさとして正しいものを以下の選択肢から選びなさい。 $\sqrt{2}$$2$$3$$\sqrt{3}$解説を見るギブアップ...次の問題へ進む閉じる問題 以下の立方体 ${\rm ABCDEFGH}$ において, $|\overrightarrow{{\rm AB}}|=1$ の時, $\overrightarrow{{\rm AG}}$ の大きさとして正しいものを以下の選択肢から選びなさい。 $\sqrt{3}$$\sqrt{2}$$2$$3$解説を見るギブアップ...次の問題へ進む閉じる問題 以下の立方体 ${\rm ABCDEFGH}$ において, $|\overrightarrow{{\rm AB}}|=1$ の時, $\overrightarrow{{\rm HD}}$ の大きさとして正しいものを以下の選択肢から選びなさい。 $1$$2$$\sqrt{2}$$\sqrt{3}$解説を見るギブアップ...次の問題へ進む閉じる問題 以下の立方体 ${\rm ABCDEFGH}$ において, $|\overrightarrow{{\rm AD}}|=1$ の時, $\overrightarrow{{\rm DF}}$ の大きさとして正しいものを以下の選択肢から選びなさい。 $\sqrt{3}$$1$$2$$\sqrt{2}$解説を見るギブアップ...次の問題へ進む閉じる問題 以下の立方体 ${\rm ABCDEFGH}$ において, $|\overrightarrow{{\rm AD}}|=1$ の時, $\overrightarrow{{\rm CH}}$ の大きさとして正しいものを以下の選択肢から選びなさい。 $\sqrt{2}$$2$$1$$\sqrt{3}$解説を見るギブアップ...次の問題へ進む閉じる premium 学習コース 数学チャンネル（線形代数 I） 9. 空間ベクトルの成分 練習問題一覧 空間ベクトルの相等 空間ベクトルの大きさ1 空間ベクトルの大きさ2 空間ベクトルの逆ベクトル 空間ベクトルの成分表示 空間ベクトルの相等（成分表示） 空間ベクトルの大きさ（成分表示）1 空間ベクトルの計算 空間ベクトルの大きさ（成分表示）2 空間ベクトルの線形結合 空間における内分点・外分点 前の問題で復習！！ ベクトルの大きさ 2
