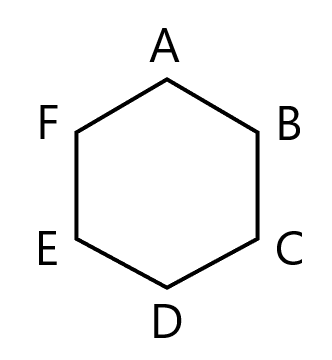
正六角形 ${\rm ABCDEF}$ において, $|\overrightarrow{{\rm AB}}| = 1$ の時, 単位ベクトルであるものを以下の選択肢から選びなさい。
$\overrightarrow{{\rm EF}}$
$\overrightarrow{{\rm AC}}$
$\overrightarrow{{\rm DA}}$
$\overrightarrow{{\rm FB}}$
大きさが $1$ であるベクトルを単位ベクトルという。$|\overrightarrow{{\rm AB}}|=1$ の時
$|\overrightarrow{{\rm EF}}| = 1$
$|\overrightarrow{{\rm AC}}| = \sqrt{3}$
$|\overrightarrow{{\rm DA}}| = 2$
$|\overrightarrow{{\rm FB}}| = \sqrt{3}$
であるから, $|\overrightarrow{{\rm EF}}|$ は単位ベクトルである。
正六角形 ${\rm ABCDEF}$ において, $|\overrightarrow{{\rm AC}}| = \dfrac{\sqrt{3}}{2}$ の時, 単位ベクトルであるものを以下の選択肢から選びなさい。

$\overrightarrow{{\rm FC}}$
$\overrightarrow{{\rm AB}}$
$\overrightarrow{{\rm AE}}$
$\overrightarrow{{\rm EC}}$
大きさが $1$ であるベクトルを単位ベクトルという。$|\overrightarrow{{\rm AC}}| = \dfrac{\sqrt{3}}{2}$ の時
$|\overrightarrow{{\rm FC}}| = 1$
$|\overrightarrow{{\rm AB}}| = \dfrac{1}{2}$
$|\overrightarrow{{\rm AE}}| = |\overrightarrow{{\rm EC}}| = \dfrac{\sqrt{3}}{2}$
であるので, $\overrightarrow{{\rm FC}}$ は単位ベクトルである。
正六角形 ${\rm ABCDEF}$ において, $|\overrightarrow{{\rm FA}}| = \dfrac{1}{2}$ の時, 単位ベクトルであるものを以下の選択肢から選びなさい。

$\overrightarrow{{\rm DA}}$
$\overrightarrow{{\rm AE}}$
$\overrightarrow{{\rm BA}}$
$\overrightarrow{{\rm DF}}$
大きさが $1$ であるベクトルを単位ベクトルという。$|\overrightarrow{{\rm FA}}|=\dfrac{1}{2}$ の時
$|\overrightarrow{{\rm DA}}| = 1$
$|\overrightarrow{{\rm BA}}| = \dfrac{1}{2}$
$|\overrightarrow{{\rm AE}}| = |\overrightarrow{{\rm DF}}| = \dfrac{\sqrt{3}}{2}$
であるから, $|\overrightarrow{{\rm DA}}|$ は単位ベクトルである。
正六角形 ${\rm ABCDEF}$ において, $|\overrightarrow{{\rm DC}}| = \dfrac{1}{\sqrt{3}}$ の時, 単位ベクトルであるものを以下の選択肢から選びなさい。

$\overrightarrow{{\rm FD}}$
$\overrightarrow{{\rm BE}}$
$\overrightarrow{{\rm CF}}$
$\overrightarrow{{\rm AB}}$
大きさが $1$ であるベクトルを単位ベクトルという。$|\overrightarrow{{\rm DC}}|= \dfrac{1}{\sqrt{3}}$ の時
$|\overrightarrow{{\rm FD}}| = 1$
$|\overrightarrow{{\rm AB}}| = \dfrac{1}{\sqrt{3}}$
$|\overrightarrow{{\rm BE}}| = |\overrightarrow{{\rm CF}}| = \dfrac{2}{\sqrt{3}}$
であるから, $|\overrightarrow{{\rm FD}}|$ は単位ベクトルである。
