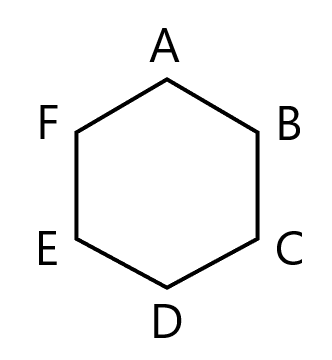
正六角形 ${\rm ABCDEF}$ において, $\overrightarrow{{\rm AF}}$ と等しいベクトルを以下の選択肢から選びなさい。
$\overrightarrow{{\rm CD}}$
$\overrightarrow{{\rm BE}}$
$\overrightarrow{{\rm AE}}$
$\overrightarrow{{\rm FA}}$
大きさと向きが同じである時に $2$ つのベクトルは等しいという。
$\overrightarrow{{\rm BE}}$ は大きさが違い, $\overrightarrow{{\rm FA}}$ は向きが反対なので等しいベクトルではない。
正六角形 ${\rm ABCDEF}$ において, $\overrightarrow{{\rm FB}}$ と等しいベクトルを以下の選択肢から選びなさい。

$\overrightarrow{{\rm EC}}$
$\overrightarrow{{\rm AD}}$
$\overrightarrow{{\rm CE}}$
$\overrightarrow{{\rm AB}}$
大きさと向きが同じである時に $2$ つのベクトルは等しいという。
$\overrightarrow{{\rm CE}}$ は向きが反対なので等しいベクトルではない。
正六角形 ${\rm ABCDEF}$ において, $\overrightarrow{{\rm AE}}$ と等しいベクトルを以下の選択肢から選びなさい。

$\overrightarrow{{\rm BD}}$
$\overrightarrow{{\rm ED}}$
$\overrightarrow{{\rm DB}}$
$\overrightarrow{{\rm CD}}$
大きさと向きが同じである時に $2$ つのベクトルは等しいという。
$\overrightarrow{{\rm DB}}$ は向きが反対なので等しいベクトルではない。
正六角形 ${\rm ABCDEF}$ において, $\overrightarrow{{\rm AC}}$ と等しいベクトルを以下の選択肢から選びなさい。

$\overrightarrow{{\rm FD}}$
$\overrightarrow{{\rm ED}}$
$\overrightarrow{{\rm DF}}$
$\overrightarrow{{\rm AD}}$
大きさと向きが同じである時に $2$ つのベクトルは等しいという。
$\overrightarrow{{\rm DF}}$ は向きが反対なので等しいベクトルではない。
正六角形 ${\rm ABCDEF}$ において, $\overrightarrow{{\rm AB}}$ と等しいベクトルを以下の選択肢から選びなさい。

$\overrightarrow{{\rm ED}}$
$\overrightarrow{{\rm FD}}$
$\overrightarrow{{\rm BA}}$
$\overrightarrow{{\rm CD}}$
大きさと向きが同じである時に $2$ つのベクトルは等しいという。
$\overrightarrow{{\rm BA}}$ は向きが反対なので等しいベクトルではない。
