$Q1$.
以下の問いに答えなさい。
解答・解説を見る$Q2$.
次の極方程式で表される図形の, (直交座標における) 方程式を求めなさい。
解答・解説を見る(1)
直交座標と極座標の関係から
$\sqrt{x^2 + y^2} = r = 4$
両辺を $2$ 乗すれば
$x^2 + y^2 = 16$
よってこの図形は原点を中心とする半径 $4$ の円であることがわかります。
(2)
加法定理を用いると
$rsin(θ−π2)=r(1√2sinθ−1√2cosθ)=1√2(rsinθ−rcosθ)=1√2(y−x)$
よって
$\dfrac{1}{\sqrt{2}}\left( y-x\right) = \dfrac{1}{\sqrt{2}}$
両辺を $\sqrt{2}$ 倍して整理すれば $y = x+1$ となります。
よってこの図形は傾きが $1$ で $y$ 切片が $1$ の直線になります。
$Q3$.
次で表される図形の面積 $S$ を求めなさい。
解答・解説を見る極方程式 $r=f(\theta)$ と直線 $\theta = \alpha$, $\theta = \beta$ で囲まれた部分の面積 $S$ は
$\displaystyle S = \int_{\alpha}^{\beta} \dfrac{1}{2} \left\{ f(\theta)\right\}^2~d\theta$
で計算できます。
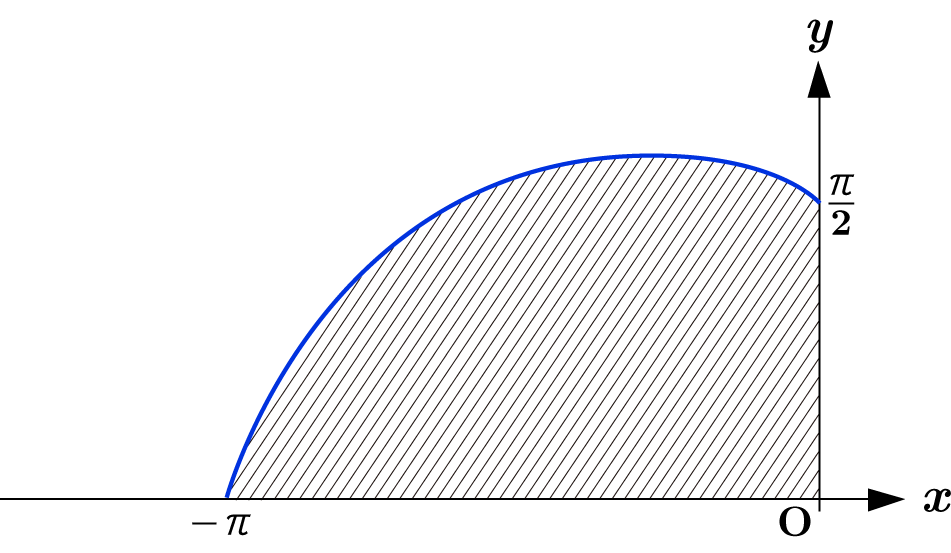
与えられた図形は上図のようになり, $x$ 軸と $y$ 軸はそれぞれ直線 $\theta = \dfrac{\pi}{2}$ と $\theta = \pi$ に一致するから面積 $S$ は
$\displaystyle S = \cfrac{1}{2} \int_{\frac{\pi }{2}}^{\pi} {\theta }^2 d\theta = \cfrac{1}{2} \left[\cfrac{1}{3} \theta ^3 \right]_{\frac{\pi }{2}}^\pi = \cfrac{7}{48} \pi^3$
$Q4$.
次で表される曲線の長さ $L$ を求めなさい。
解答・解説を見る極方程式 $r=f(\theta)~~(\alpha \leqq \theta \leqq \beta)$ で表される曲線の長さ $L$ は
$\displaystyle L = \int_{\alpha}^{\beta} \sqrt{ \left\{ f(\theta) \right\}^2 + \left\{ f'(\theta) \right\}^2 } ~ d\theta = \int_{\alpha}^{\beta} \sqrt{ r^2 + \left( r' \right)^2 } ~ d\theta$
で計算できます。
$\left( 3e^{\theta}\right)' = 3e^{\theta}$ より
$L=∫π0√(3eθ)2+(3eθ)2 dθ=∫π0√18e2θ dθ=∫π03√2 eθ dθ=[3√2 eθ]π0=3√2(eπ−1)$
ある点の直交座標が $(x,y)$ で極座標が $(r, \theta)$ である時
$\left\{ x=rcosθy=rsinθ \right.$
という関係が成り立ちます。
(1)
$x$ 座標と $y$ 座標をそれぞれ求めると
$x = r\cos \theta = \cos \dfrac{\pi}{6} = \dfrac{\sqrt{3}}{2}$
$y = r\sin \theta = \sin \dfrac{\pi}{6} = \dfrac{1}{2}$
よってこの点の直交座標は $\left( \dfrac{\sqrt{3}}{2},~\dfrac{1}{2} \right)$ となります。
(2)
直交座標と極座標の関係から
$x^2 + y^2 = r^2$
が成り立つので
$r^2 = x^2 + y^2 = \left(\sqrt{2}\right)^2 + \left(\sqrt{2}\right)^2 = 4$
$r \gt 0$ より $r=2$ となります。また
$\cos \theta = \dfrac{x}{r} = \dfrac{\sqrt{2}}{2}$
$\sin \theta = \dfrac{y}{r} = \dfrac{\sqrt{2}}{2}$
であるから, これを満たす $\theta$ は $\theta = \dfrac{\pi}{4}$ であることがわかります。
よってこの点の極座標は $\left( 2,~\dfrac{\pi}{4} \right)$ となります。