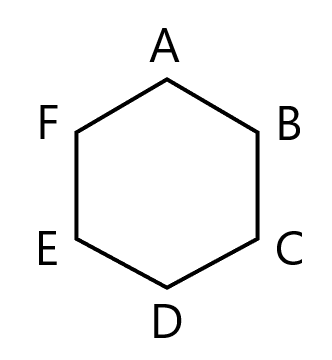
正六角形 ${\rm ABCDEF}$ において, $|\overrightarrow{{\rm AB}} |=1$ の時, $\overrightarrow{{\rm DE}}$ の大きさとして最も適切なものを以下の選択肢から選びなさい。
$1$
$\sqrt{3}$
$2$
$\dfrac{1}{2}$
$|\overrightarrow{{\rm AB}} |= |\overrightarrow{{\rm DE}} |$ より, $|\overrightarrow{{\rm DE}} | =1$ である。
正六角形 ${\rm ABCDEF}$ において, $|\overrightarrow{{\rm AD}} |=2$ の時, $\overrightarrow{{\rm AE}}$ の大きさとして最も適切なものを以下の選択肢から選びなさい。

$\sqrt{3}$
$1$
$2$
$\dfrac{\sqrt{3}}{2}$
$\angle~{\rm ADE} = \dfrac{\pi}{3}$ かつ $\angle~{\rm AED} = \dfrac{\pi}{2}$ より
$|\overrightarrow{{\rm AE}}| = |\overrightarrow{{\rm AD}}| \sin \dfrac{\pi}{3} = \sqrt{3}$
である。
正六角形 ${\rm ABCDEF}$ において, $|\overrightarrow{{\rm BC}} |=2$ の時, $\overrightarrow{{\rm CE}}$ の大きさとして最も適切なものを以下の選択肢から選びなさい。

$2\sqrt{3}$
$4$
$\sqrt{3}$
$3$
$\angle~{\rm EBC} = \dfrac{\pi}{3}$ かつ $\angle~{\rm ECB} = \dfrac{\pi}{2}$ より
$|\overrightarrow{{\rm CE}}| = |\overrightarrow{{\rm BC}}| \tan \dfrac{\pi}{3} = 2\sqrt{3}$
よって $|\overrightarrow{{\rm CE}}| = 2\sqrt{3}$ である。
正六角形 ${\rm ABCDEF}$ において, $|\overrightarrow{{\rm AC}} |=\sqrt{3}$ の時, $\overrightarrow{{\rm FA}}$ の大きさとして最も適切なものを以下の選択肢から選びなさい。

$1$
$\dfrac{1}{\sqrt{3}}$
$\dfrac{1}{2}$
$\dfrac{\sqrt{3}}{2}$
$\angle~{\rm ACF} = \dfrac{\pi}{6}$ かつ $\angle~{\rm CAF} = \dfrac{\pi}{2}$ であるから,
$|\overrightarrow{{\rm FA}}| = |\overrightarrow{{\rm AC}}| \tan \dfrac{\pi}{6}$
よって $|\overrightarrow{{\rm FA}}| = \dfrac{\sqrt{3}}{\sqrt{3}}=1$ である。
正六角形 ${\rm ABCDEF}$ において, $|\overrightarrow{{\rm CF}} |=1$ の時, $\overrightarrow{{\rm AB}}$ の大きさとして最も適切なものを以下の選択肢から選びなさい。

$\dfrac{1}{2}$
$1$
$\dfrac{1}{\sqrt{3}}$
$\dfrac{1}{4}$
${\rm ABCDEF}$ は正六角形であるから, $|\overrightarrow{{\rm CF}}| = 2|\overrightarrow{{\rm AB}}|$ である。
よって $|\overrightarrow{{\rm AB}}| = \dfrac{1}{2}$ である。
