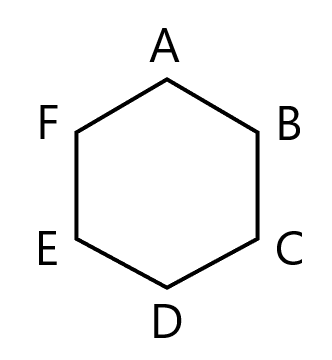
正六角形 ${\rm ABCDEF}$ において, $\overrightarrow{{\rm AB}}$ の逆ベクトルと等しいものを以下の選択肢から選びなさい。
$\overrightarrow{{\rm DE}}$
$\overrightarrow{{\rm AB}}$
$\overrightarrow{{\rm CF}}$
$\overrightarrow{{\rm DA}}$
ベクトル $\overrightarrow{a}$ に対し, $\overrightarrow{a}$ と大きさが等しく, 向きが反対のベクトルを $\overrightarrow{a}$ の逆ベクトルといい $-\overrightarrow{a}$ と表す。
特に, 始点と終点を逆にしたベクトルは元のベクトルの逆ベクトルになる。
$\overrightarrow{{\rm CF}}$ は大きさが異なるので $\overrightarrow{{\rm AB}}$ の逆ベクトルではない。
正六角形 ${\rm ABCDEF}$ において, $\overrightarrow{{\rm FD}}$ の逆ベクトルを以下の選択肢から選びなさい。

$\overrightarrow{{\rm CA}}$
$\overrightarrow{{\rm BA}}$
$\overrightarrow{{\rm AC}}$
$\overrightarrow{{\rm EF}}$
ベクトル $\overrightarrow{a}$ に対し, $\overrightarrow{a}$ と大きさが等しく, 向きが反対のベクトルを $\overrightarrow{a}$ の逆ベクトルといい $-\overrightarrow{a}$ と表す。
特に, 始点と終点を逆にしたベクトルは元のベクトルの逆ベクトルになる。
$\overrightarrow{{\rm AC}}$ は $\overrightarrow{{\rm FD}}$ と等しいベクトルなので逆ベクトルではない。
正六角形 ${\rm ABCDEF}$ において, $\overrightarrow{{\rm BE}}$ の逆ベクトルを以下の選択肢から選びなさい。

$\overrightarrow{{\rm EB}}$
$\overrightarrow{{\rm CD}}$
$\overrightarrow{{\rm EA}}$
$\overrightarrow{{\rm FA}}$
ベクトル $\overrightarrow{a}$ に対し, $\overrightarrow{a}$ と大きさが等しく, 向きが反対のベクトルを $\overrightarrow{a}$ の逆ベクトルといい $-\overrightarrow{a}$ と表す。
特に, 始点と終点を逆にしたベクトルは元のベクトルの逆ベクトルになる。
他の選択肢はいずれも大きさが異なるので $\overrightarrow{{\rm BE}}$ の逆ベクトルではない。
正六角形 ${\rm ABCDEF}$ において, $-\overrightarrow{{\rm AB}}$ と等しいベクトルを以下の選択肢から選びなさい。

$\overrightarrow{{\rm BA}}$
$\overrightarrow{{\rm AB}}$
$\overrightarrow{{\rm AC}}$
$\overrightarrow{{\rm CF}}$
ベクトル $\overrightarrow{a}$ に対し, $\overrightarrow{a}$ と大きさが等しく, 向きが反対のベクトルを $\overrightarrow{a}$ の逆ベクトルといい $-\overrightarrow{a}$ と表す。
特に, 始点と終点を逆にしたベクトルは元のベクトルの逆ベクトルになるので $-\overrightarrow{{\rm AB}} = \overrightarrow{{\rm BA}}$ である。
$\overrightarrow{{\rm CF}}$ は $-\overrightarrow{{\rm AB}}$ と大きさが異なるので逆ベクトルではない。
正六角形 ${\rm ABCDEF}$ において, $-\overrightarrow{{\rm CA}}$ と等しいベクトルを以下の選択肢から選びなさい。

$\overrightarrow{{\rm FD}}$
$\overrightarrow{{\rm BA}}$
$\overrightarrow{{\rm CA}}$
$\overrightarrow{{\rm BC}}$
ベクトル $\overrightarrow{a}$ に対し, $\overrightarrow{a}$ と大きさが等しく, 向きが反対のベクトルを $\overrightarrow{a}$ の逆ベクトルといい $-\overrightarrow{a}$ と表す。
特に, 始点と終点を逆にしたベクトルは元のベクトルの逆ベクトルになる。
よって $-\overrightarrow{{\rm CA}} = \overrightarrow{{\rm AC}}$ であり, $\overrightarrow{{\rm AC}}$ と等しいベクトルは $\overrightarrow{{\rm FD}}$ である。
