長方形領域 $D:a \leqq x \leqq b,~c\leqq y \leqq d$ における $2$ 重積分は

$ $$\begin{eqnarray*} \iint_D f(x,y)~dxdy & = & \int_c^d \left\{ \int_a^b f(x,y)~dx\right\}~dy\\[1em] & = & \int_a^b \left\{ \int_c^d f(x,y)~dy\right\}~dx\end{eqnarray*}$$ $

と計算することができます。

偏微分の時と同様に, 片方の変数に関して積分している時は, もう一方の変数は定数として扱うことに注意しましょう。

(1)

$ $$\begin{eqnarray*}\iint_D (xy+x) ~ dxdy & = & \displaystyle{\int_{-2}^{2} \left\{\int_{1}^{2}(xy+x)\ dx\right\}\ dy}\\[1em] & = & \int_{-2}^{2} \left[\cfrac{1}{2}(y+1)~ x^2 \right]_1^2 \ dy\\[1em] & = & \int_{-2}^{2} \cfrac{3}{2}(y+1)\ dy\\[1em] & = & \cfrac{3}{2}\left[\cfrac{1}{2} y^2+y\right]_{-2}^2 = 6 \end{eqnarray*}$$ $

(2)

$ $$\begin{eqnarray*} \iint_D \dfrac{x}{y}\, dxdy & = & \displaystyle{\int_{1}^{e^2} \left\{\int_{3}^{7}\cfrac{x}{y} \ dx\right\}\ dy}\\[1em] & = & \int_{1}^{e^2} \left[\cfrac{1}{2y} x^2\right]_3^7 \ dy\\[1em] & = & \int_{1}^{e^2} \cfrac{20}{y} \ dy = 20\left[\ \log y\ \right]_1^{e^2} = 40 \end{eqnarray*}$$ $

(3)
積分しやすそうな $y$ から積分してみましょう。

$ $$\begin{eqnarray*} \iint_D \sin (x+y)\, dxdy & = & \displaystyle{\int_{-\frac{\pi}{6}}^{\frac{\pi}{6}} \left\{\int_{0}^{\pi} \sin (x+y)\ dy\right\}\ dx}\\[1em] & = & \int_{-\frac{\pi}{6}}^{\frac{\pi}{6}} \left[-\cos (x+y)\right]_0^\pi \ dx\\[1em] & = & \int_{-\frac{\pi}{6}}^{\frac{\pi}{6}} \left( -\cos (x+\pi) + \cos x \right) \ dx\\[1em] & = & \int_{-\frac{\pi}{6}}^{\frac{\pi}{6}} 2\cos x\ dx\\[1em] & = & 2\int_0^{\frac{\pi}{6}} 2\cos x\ dx = 4\left[\ \sin x\ \right]_{0}^{\frac{\pi }{6}} = 2 \end{eqnarray*}$$ $

領域 $D$ が

$D:a \leqq x \leqq b,~g_1(x)\leqq y \leqq g_2(x)$

のように $y$ の区間が $x$ の関数を用いて表されている時, $D$ における $2$ 重積分は

$\displaystyle \iint_D f(x,y)~dxdy = \int_a^b \left\{ \int_{g_1(x)}^{g_2(x)} f(x,y)~dy\right\}~dx$

と計算することができます。同様に, 領域 $D$ が

$D:h_1(y) \leqq x \leqq h_2(y),~c \leqq y \leqq d$

のように $x$ の区間が $y$ の関数を用いて表されている時, $D$ における $2$ 重積分は

$\displaystyle \iint_D f(x,y)~dxdy = \int_c^d \left\{ \int_{h_1(y)}^{h_2(y)} f(x,y)~dx\right\}~dy$

と計算することができます。

(1)
$y$ から積分していきます。

$ $$\begin{eqnarray*} \iint_D (x+y) \, dxdy & = & \displaystyle{\int_{1}^{2} \left\{\int_{0}^{x^2}(y+x) \ dy\right\}\ dx}\\[1em] & = & \int_{1}^{2} \left[\cfrac{1}{2} y^2 + xy \right]_0^{x^2} \ dx\\[1em] & = & \int_{1}^{2} \left(\cfrac{1}{2} x^4+x^3 \right)\ dx\\[1em] & = & \left[\cfrac{1}{10} x^5+\cfrac{1}{4} x^4 \right]_1^2 = \cfrac{137}{20} \end{eqnarray*}$$ $

(2)
$x$ から積分していきます。

$ $$\begin{eqnarray*} \iint_D (x+y) \,dxdy & = & \displaystyle{\int_{1}^{4} \left\{\int_{1}^{\sqrt{y}}(x+y) \ dx\right\}\ dy}\\[1em] & = & \int_{1}^{4} \left[\cfrac{1}{2} x^2+xy\right]_1^{\sqrt{y}} \ dy\\[1em] & = & \int_{1}^{4} \left(\cfrac{1}{2} y+y\sqrt{y}-\cfrac{1}{2}-y\right)\ dy\\[1em] & = & \int_{1}^{4} \left(y^{\frac{3}{2}}-\cfrac{1}{2} y-\cfrac{1}{2}\right)\ dy\\[1em] & = & \left[\cfrac{2}{5} y^{\frac{5}{2}}-\cfrac{1}{4} y^2-\cfrac{1}{2} y\right]_1^4 = \cfrac{34}{5} -\left(-\dfrac{7}{20}\right) = \dfrac{143}{20} \end{eqnarray*}$$ $

(3)
$y$ から積分していきます。

$ $$\begin{eqnarray*} \iint_D \cos (x+y) \, dxdy & = & \displaystyle{\int_{0}^{\pi} \left\{\int_{-\pi}^{x} \cos (x+y)\ dy\right\}\ dx}\\[1em] & = & \int_{0}^{\pi} \left[\sin (x+y)\right]_{-\pi }^x \ dx\\[1em] & = & \int_{0}^{\pi} \left( \sin 2x - \sin (x-\pi) \right)\ dx\\[1em] & = & \int_{0}^{\pi} (\sin 2x+\sin x)\ dx\\[1em] & = & \left[-\cfrac{1}{2} \cos 2x-\cos x\right]_0^\pi = 2 \end{eqnarray*}$$ $

領域 $D$ が

$D:a \leqq x \leqq b,~g_1(x)\leqq y \leqq g_2(x)$

であり, また

$D:h_1(y) \leqq x \leqq h_2(y),~c\leqq y \leqq d$

と表せている時, どちらの表し方をしても $2$ 重積分 $\displaystyle \iint_D f(x,y)~dxdy$ の値は等しくなります。すなわち

$\displaystyle \int_a^b \left\{ \int_{g_1(x)}^{g_2(x)} f(x,y)~dy\right\}~dx = \int_c^d \left\{ \int_{h_1(y)}^{h_2(y)} f(x,y)~dx\right\}~dy$

が成り立ちます。このような操作を 積分順序を交換する といいます。

積分順序を交換する時は, 積分領域を図示してから範囲を求めるようにしましょう。

(1)
積分範囲は

$D:0 \leqq x \leqq 4,~2 \leqq y \leqq \dfrac{1}{2}x+2$

であり, これを図示すると下のようになります。

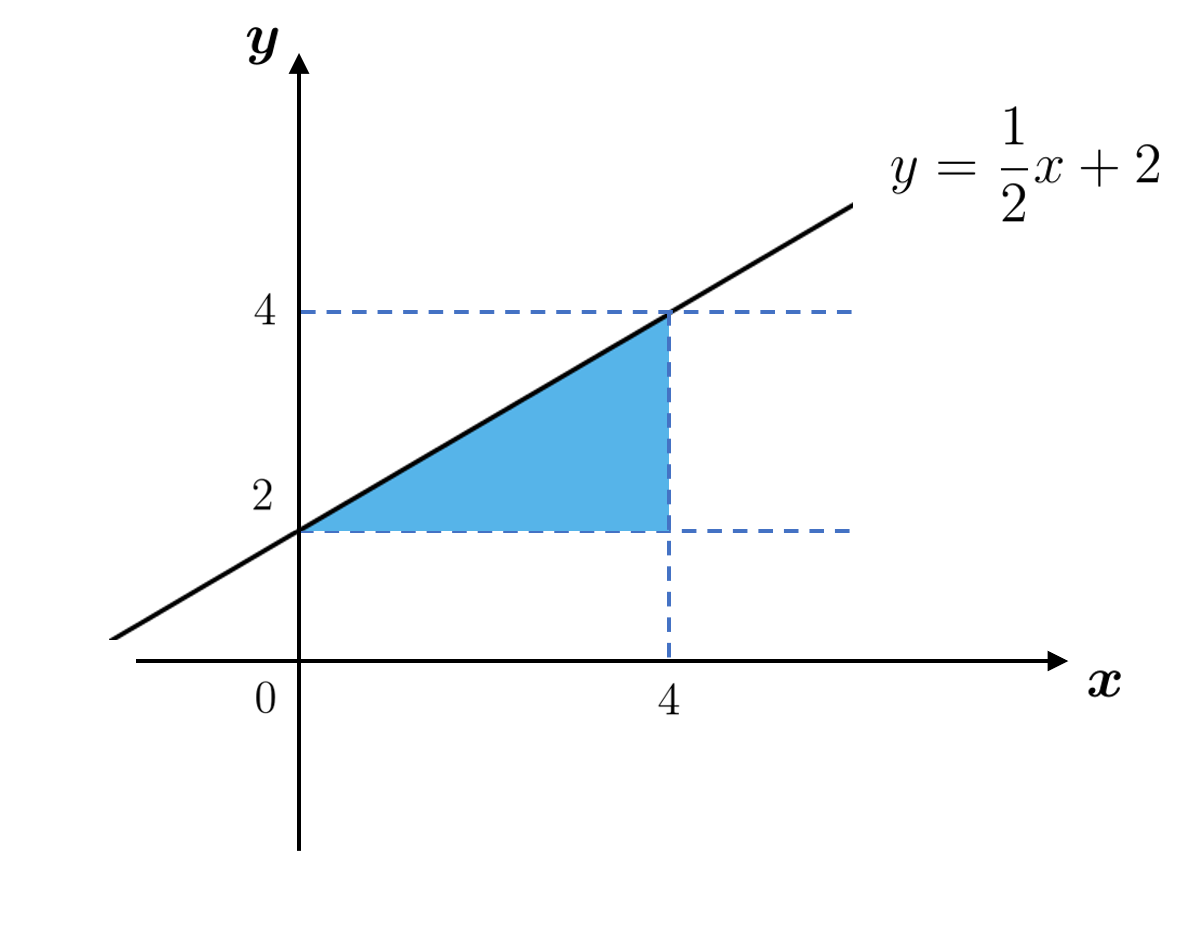
よって $2 \leqq y \leqq 4$ であり, $y =\dfrac{1}{2}x+2$ を $x$ について解くと

$x = 2y-4$

であるから, $2y-4 \leqq x \leqq 4$ となります。以上から

$\displaystyle \int_0^4\left\{ \int_{2}^{\frac{1}{2}x+2} f(x,y)~dy\right\} ~dx = \int_2^4\left\{ \int_{2y-4}^{4} f(x,y)~dx\right\} ~dy$

となります。

(2)
積分範囲は

$D:\sqrt{y} \leqq x \leqq 1,~0 \leqq y \leqq 1$

$\sqrt{y} = x$ の時, $y = x^2$ であることに注意すると, この領域は下のようになります。

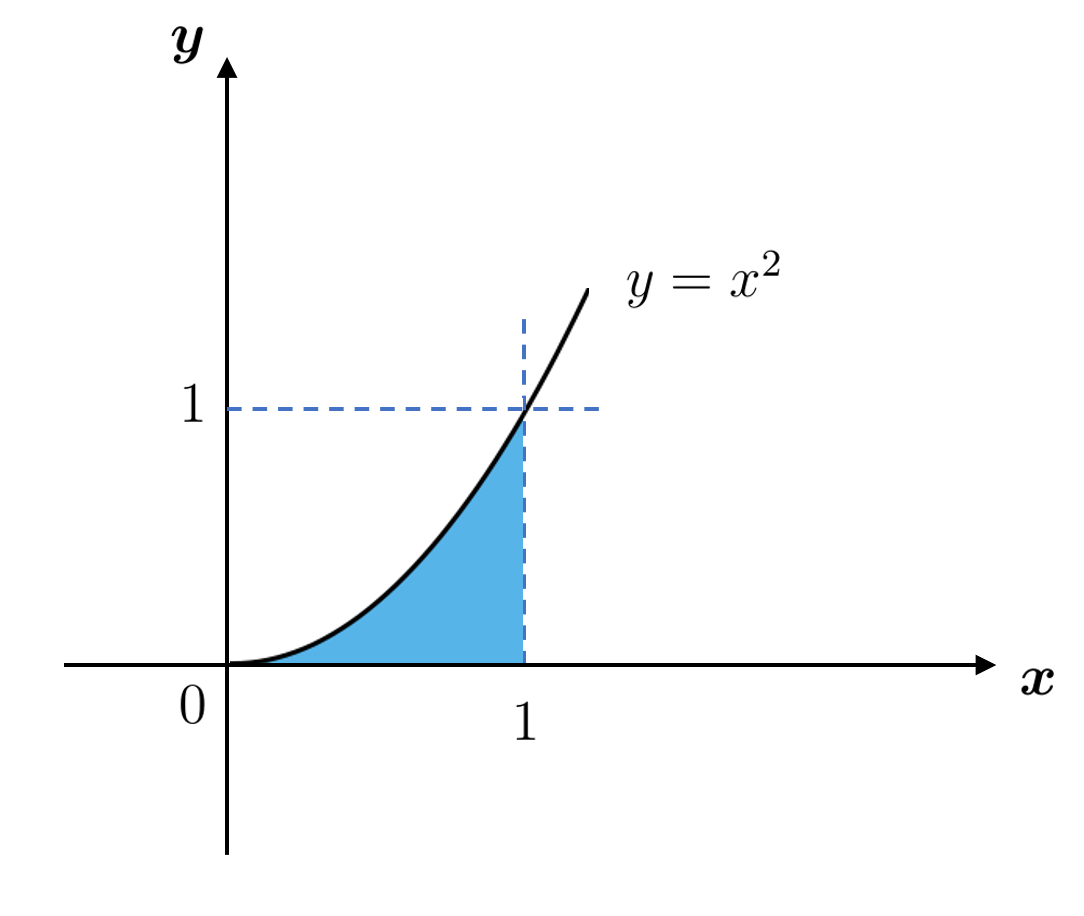
よって $0 \leqq x \leqq 1$ かつ $0 \leqq y \leqq x^2$ となるので, $2$ 重積分は

$\displaystyle \int_0^1\left\{ \int_{\sqrt{y}}^{1} f(x,y)~dx\right\} ~dy = \int_0^1\left\{ \int_{0}^{x^2} f(x,y)~dy\right\} ~dx$

となります。

(3)
積分範囲は

$D:1 \leqq x \leqq e^2,~0 \leqq y \leqq \log x$

であり $\log e^2 = 2$ より, これを図示すると下のようになります。

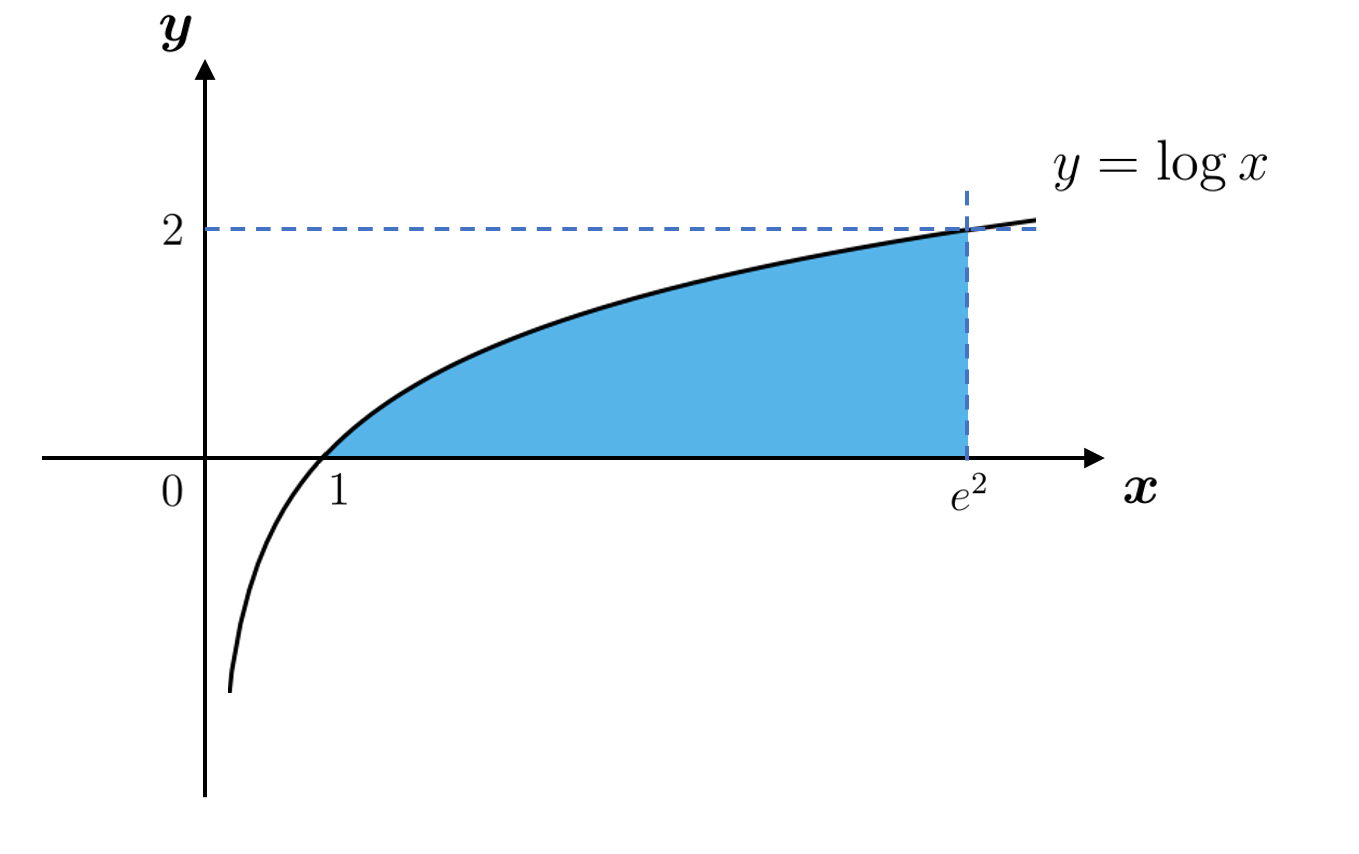
よって $0 \leqq y \leqq 2$ であり, $x = e^y$ より

$ e^y \leqq x \leqq e^2$

となります。以上から $2$ 重積分は

$\displaystyle \int_1^{e^2}\left\{ \int_{0}^{\log x} f(x,y)~dy\right\} ~dx = \int_0^2\left\{ \int_{e^y}^{e^2} f(x,y)~dx\right\} ~dy$

となります。

積分するのが難しい関数でも, 積分順序を交換することで積分できるようになることがあります。

領域 $D$ は

$D:y \leqq x \leqq 1,~0\leqq y \leqq 1$

より, 図示すると下のようになります。

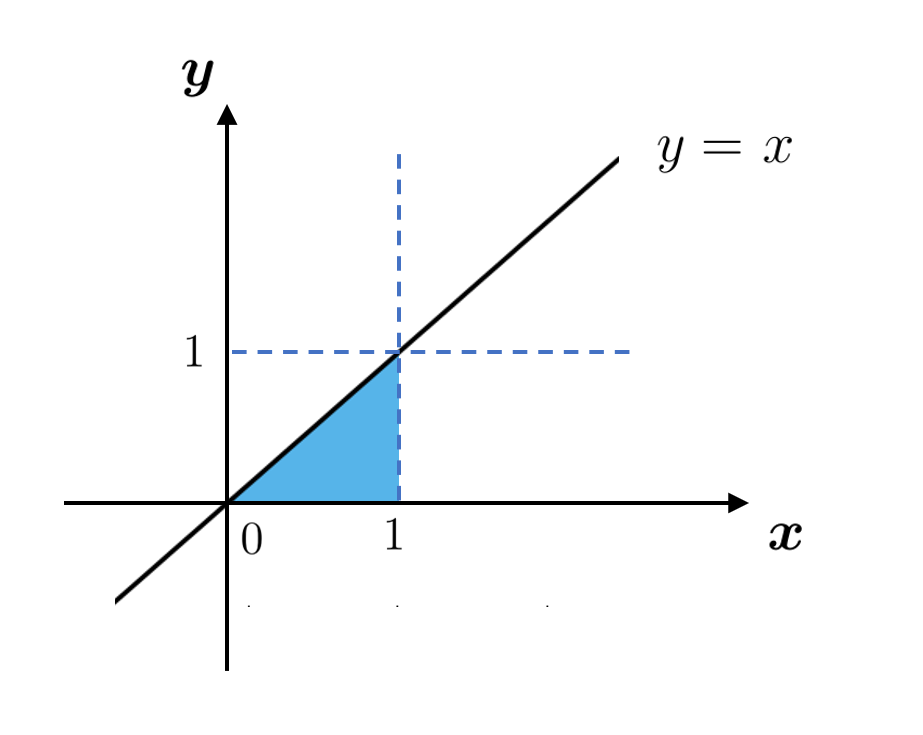
図から $D:0 \leqq x \leqq 1,~0 \leqq y \leqq x$ であるので, $2$ 重積分は

$ $$\begin{eqnarray*}\int_0^1\left\{ \int_{y}^{1} e^{x^2}~dx \right\} ~dy & = & \int_0^1\left\{ \int_{0}^{x} e^{x^2}~dy \right\} ~dx\\[1em] & = & \int_0^1 \left[ ye^{x^2} \right]_0^x ~ dx\\[1em] & = & \int_0^1 xe^{x^2} ~ dx\\[1em] & = & \left[ \dfrac{1}{2}e^{x^2} \right]_0^1 = \dfrac{1}{2}(e-1) \end{eqnarray*}$$ $