点 $(-1,-3)$ を通り $y$ 軸に平行な直線の方程式は $x=-1$ であり,

この直線は円 $x^2 + y^2 = 2$ と $2$ 点 $(-1,1)$, $(-1,-1)$ で交わります。

よって直線 $x=-1$ は接線ではないことがわかります。

接線の方程式を $y = ax+b$ とすると $(-1,-3)$ を通るので

$-3 = -a + b$

より $b =a-3$ となります。接線の方程式に代入すると

$y = a(x+1)-3$

これを円の方程式に代入すると

$x^2 + \left( a(x+1)-3 \right)^2 =2$

展開して整理すると

$(a^2+1)x^2 + 2a(a-3)x + (a^2-6a+7) = 0$

となります。接線との共有点は $1$ 点であることから, この $x$ に関する $2$ 次方程式は唯一つの解を持ちます。

よって判別式を $D$ とすると

$D = 4a^2(a-3)^2 -4(a^2+1)(a^2-6a+7) = 0$

ここで

$a^2(a-3)^2 = a^4-6a^3+9a^2$

また

$(a^2+1)(a^2-6a+7) = a^4-6a^3 + 8a^2 -6a + 7$

であるから

$ $$\begin{eqnarray*}D & = & 4(a^4-6a^3+9a^2) - 4(a^4-6a^3 + 8a^2 -6a + 7)\\[0.5em] & = & 4(a^2 +6a - 7)=0\end{eqnarray*}$$ $

$a^2+6a-7=(a+7)(a-1)=0$ より $a=-7,1$ となります。

それぞれ接線の方程式に代入すれば, 求める接線の方程式は

$ $$\begin{eqnarray*}y & = & -7x-10\\[0.5em] y & = & x-2\end{eqnarray*}$$ $

となります。

※ 求める接線が $y$ 軸に平行であるならば $y = ax+b$ という形で置くことができないので, 最初に場合分けをして考えています。

$y=x-2$ を円の方程式 $x^2 + y^2=2$ に代入すると

$x^2 + (x-2)^2 = 2$

展開して整理すると

$ $$\begin{eqnarray*}x^2 -2x +1 & = &0\\[0.5em] (x-1)^2 &= & 0\end{eqnarray*}$$ $

よって $x=1$, $y=1-2=-1$ であり, 共有点の座標は $(1,-1)$ となります。

$y = -4x+k$ を放物線の方程式に代入すると

$(-4x + k)^2 = -16x$

展開して整理すると

$16x^2 + (16-8k)x + k^2 = 0$

共有点が $1$ であればよいので, 判別式を $D$ とすると

$ $$\begin{eqnarray*}D & = & (16-8k)^2 - 4\cdot 16\cdot k^2\\[0.5em] & = & 64\left((4-4k+k^2)-k^2 \right)\\[0.5em] & = & 64(4-4k)=0\end{eqnarray*}$$ $

$4-4k=0$ より $k=1$ であればよいことがわかります。

$y = -5x+k$ を双曲線の方程式に代入すると

$\dfrac{x^2}{5} - \dfrac{(-5x+k)^2}{4} = 1$

両辺に $20$ をかけると

$4x^2 - 5(-5x+k)^2 = 20$

展開して整理すると

$121x^2 - 50kx + 5k^2 +20=0$

となります。共有点が $1$ 点なので, 判別式を $D$ とすると

$ $$\begin{eqnarray*}D & = & 2500k^2 - 4\cdot 121(5k^2+20)\\[0.5em] & = & 20\left( 125k^2 - 121(k^2+4)\right)\\[0.5em] & = & 80(k^2 - 121)=0\end{eqnarray*}$$ $

$k^2 = 121$ より $k=\pm 11$ であればよいことがわかります。

点 ${\rm A}(p,q)$ における接線を $l$ とします。

円 $(x-a)^2 + (y-b)^2 = r^2$ は, 円 $x^2+y^2=r^2$ を $x$ 軸方向に $a$, $y$ 軸方向に $b$ だけ平行移動した曲線なので

$l$ は, 円 $x^2+y^2=r^2$ 上の点 ${\rm B}(p-a,q-b)$ における接線を $x$ 軸方向に $a$, $y$ 軸方向に $b$ だけ平行移動した直線に一致します。

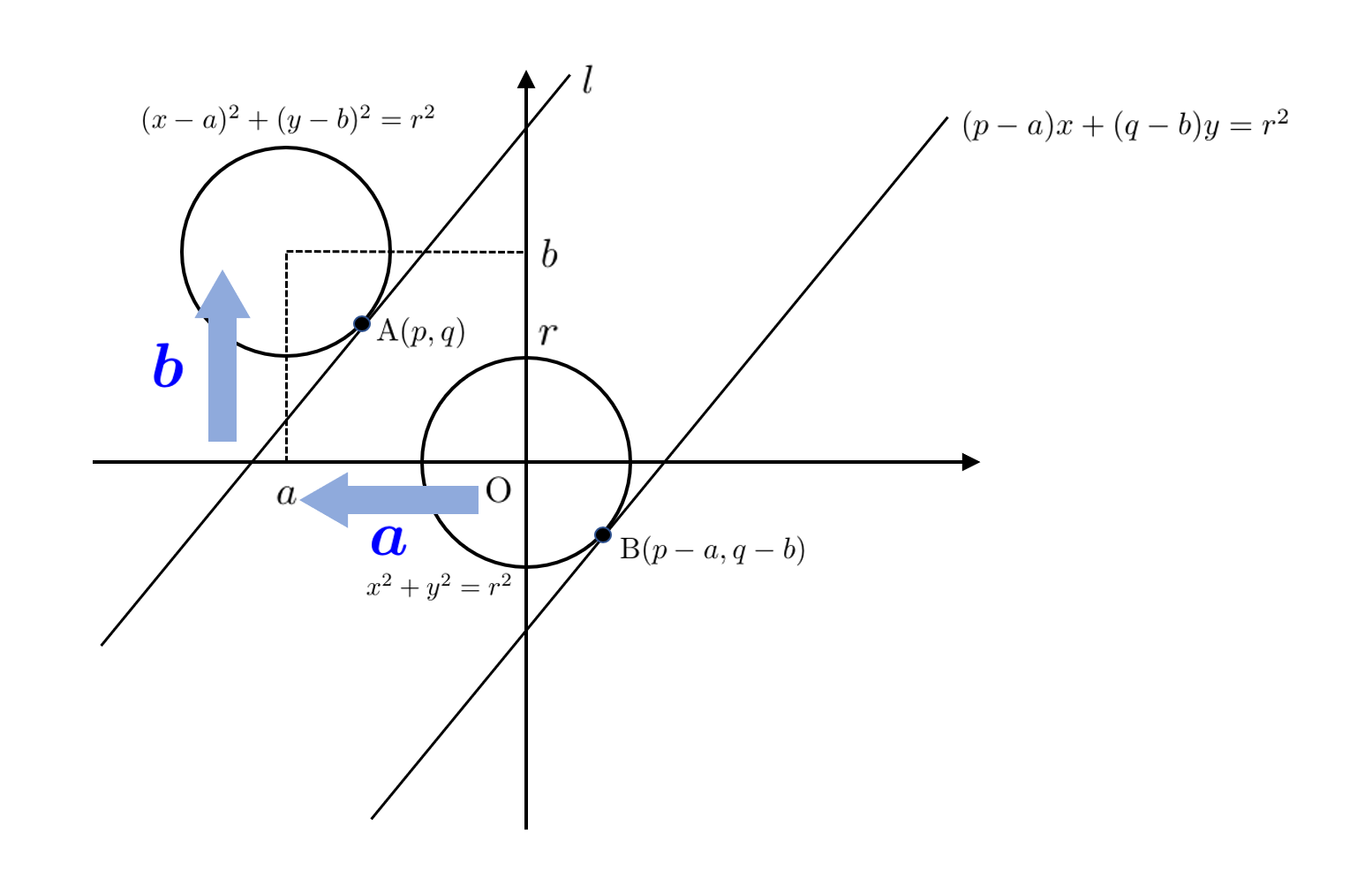
円 $x^2+y^2=r^2$ 上の点 ${\rm B}(p-a,q-b)$ における接線の方程式は

$(p-a)x + (q-b)y = r^2$

であり, この直線を $x$ 軸方向に $a$, $y$ 軸方向に $b$ だけ平行移動した直線の方程式は

$(p-a)(x-a) + (q-b)(y-b) = r^2$

となります。よってこれが $l$ の方程式となります。

$Q5$ より点 ${\rm A}$ における接線は

$(p-a)(x-a) + (q-b)(y-b) = r^2$

と表すことができます。ここで ${\rm A}$ が円上の点であることから

$r^2 = (p-a)^2 + (q-b)^2$

が成り立つので, 代入すると

$(p-a)(x-a) + (q-b)(y-b) = (p-a)^2 + (q-b)^2$

全ての項を左辺に移項し, 整理すると

$ $$\begin{eqnarray*}(p-a)(x-a) - (p-a)^2 + (q-b)(y-b) - (q-b)^2 & = & 0\\[0.5em] (p-a)\left( (x-a) - (p-a) \right) + (q-b)\left( (y-b) - (q-b) \right) & = & 0\\[0.5em] (p-a)(x-p) + (q-b)(y-q) & = & 0\end{eqnarray*}$$ $

よって点 ${\rm A}$ における接線は

$(p-a)(x-p) + (q-b)(y-q) = 0$

と表せることが分かります。