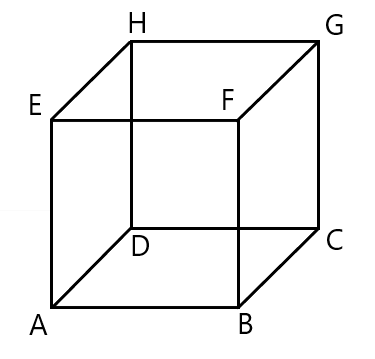
以下の立方体 ${\rm ABCDEFGH}$ において, $\overrightarrow{{\rm EH}}$ と大きさの等しいベクトルとして適切なものを以下の選択肢から選びなさい。
$\overrightarrow{{\rm AB}}$
$\overrightarrow{{\rm AC}}$
$\overrightarrow{{\rm DB}}$
$\overrightarrow{{\rm BG}}$
空間においても線分 ${\rm AB}$ の長さを, ベクトル $\overrightarrow{{\rm AB}}$ の大きさという。
${\rm ABCDEFGH}$ は立方体であるから ${\rm EH}$ と ${\rm AB}$ の長さは等しい。
以下の立方体 ${\rm ABCDEFGH}$ において, $\overrightarrow{{\rm AF}}$ と大きさの等しいベクトルとして適切なものを以下の選択肢から選びなさい。

$\overrightarrow{{\rm GB}}$
$\overrightarrow{{\rm DF}}$
$\overrightarrow{{\rm FG}}$
$\overrightarrow{{\rm AB}}$
空間においても線分 ${\rm AB}$ の長さを, ベクトル $\overrightarrow{{\rm AB}}$ の大きさという。
${\rm ABCDEFGH}$ は立方体であるから ${\rm AF}$ と ${\rm GB}$ の長さは等しい。
以下の立方体 ${\rm ABCDEFGH}$ において, $\overrightarrow{{\rm DF}}$ と大きさの等しいベクトルとして適切なものを以下の選択肢から選びなさい。

$\overrightarrow{{\rm AG}}$
$\overrightarrow{{\rm AB}}$
$\overrightarrow{{\rm AC}}$
$\overrightarrow{{\rm AD}}$
空間においても線分 ${\rm AB}$ の長さを, ベクトル $\overrightarrow{{\rm AB}}$ の大きさという。
${\rm ABCDEFGH}$ は立方体であるから ${\rm DF}$ と ${\rm AG}$ の長さは等しい。
以下の立方体 ${\rm ABCDEFGH}$ において, $\overrightarrow{{\rm BC}}$ と大きさの等しいベクトルとして適切なものを以下の選択肢から選びなさい。

$\overrightarrow{{\rm EA}}$
$\overrightarrow{{\rm FD}}$
$\overrightarrow{{\rm HF}}$
$\overrightarrow{{\rm CA}}$
空間においても線分 ${\rm AB}$ の長さを, ベクトル $\overrightarrow{{\rm AB}}$ の大きさという。
${\rm ABCDEFGH}$ は立方体であるから ${\rm BC}$ と ${\rm EA}$ の長さは等しい。
以下の立方体 ${\rm ABCDEFGH}$ において, $\overrightarrow{{\rm EC}}$ と大きさの等しいベクトルとして適切なものを以下の選択肢から選びなさい。

$\overrightarrow{{\rm HB}}$
$\overrightarrow{{\rm AB}}$
$\overrightarrow{{\rm HC}}$
$\overrightarrow{{\rm DG}}$
空間においても線分 ${\rm AB}$ の長さを, ベクトル $\overrightarrow{{\rm AB}}$ の大きさという。
${\rm ABCDEFGH}$ は立方体であるから ${\rm EC}$ と ${\rm HB}$ の長さは等しい。
