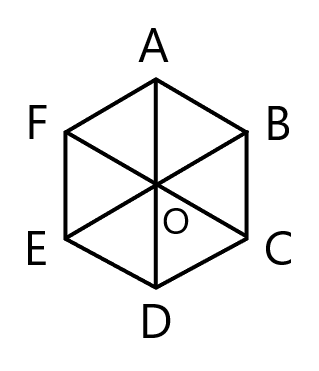
正六角形 ${\rm ABCDEF}$ において $\overrightarrow{{\rm AB}} =\overrightarrow{a}$, $\overrightarrow{{\rm AF}} =\overrightarrow{b}$ とした時, $\overrightarrow{{\rm DF}}$ を $\overrightarrow{a}$ と $\overrightarrow{b}$ を用いて表したものとして最も適切なものを以下の選択肢から選びなさい。
$-2\overrightarrow{a} - \overrightarrow{b}$
$-\dfrac{3}{2}\overrightarrow{a} - \dfrac{1}{2}\overrightarrow{b}$
$-\overrightarrow{a} - 2\overrightarrow{b}$
$-2\overrightarrow{a} + \overrightarrow{b}$
$\overrightarrow{{\rm AB}} = \overrightarrow{{\rm FO}}$ であるから
$\overrightarrow{{\rm AO}} = \overrightarrow{{\rm AF}} + \overrightarrow{{\rm FO}} = \overrightarrow{{\rm AF}} + \overrightarrow{{\rm AB}} =\overrightarrow{a}+ \overrightarrow{b}$
よって $\overrightarrow{{\rm DA}} = -\overrightarrow{{\rm AD}} = -2\overrightarrow{{\rm AO}} = -2\overrightarrow{a} - 2\overrightarrow{b}$ であるから
$\overrightarrow{{\rm DF}} = \overrightarrow{{\rm DA}} + \overrightarrow{{\rm AF}} =\left( -2\overrightarrow{a} - 2\overrightarrow{b}\right) + \overrightarrow{b} = -2\overrightarrow{a} -\overrightarrow{b}$
