14. 包絡線 例題集
$Q1$.
次の曲線群における包絡線を求めなさい。
曲線群 $f(x,y,t) = t^2x^2 + t -y=0~~$ ($t \lt 0$)
$y = -\dfrac{1}{4x^2}$
$Q2$.
次の曲線群における包絡線を求めなさい。
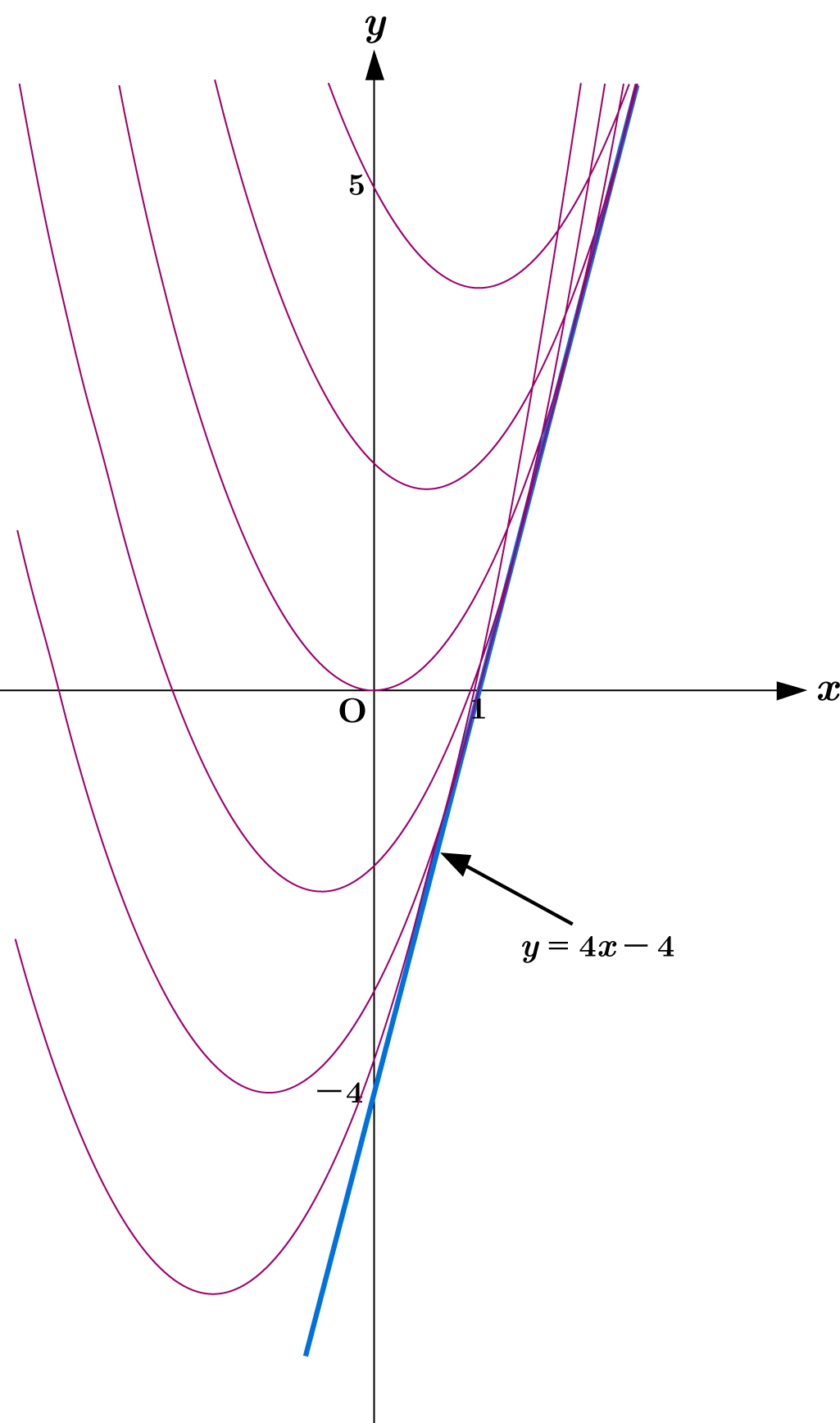
曲線群 $f(x,y,t) = (x-t)^2 + 4t -y=0$
$y = 4x - 4$
$f(x,y,t) = (x-t)^2 + 4t -y$ とすると
$f_t(x,y,t) = -2(x-t) + 4 $
より $f_t(x,y,t)=0$ とすると
$t = x-2$
$f(x,y,t)=0$ に代入すると
$4 + 4(x-2) -y =0$
よって包絡線の方程式は
$y = 4x - 4$
となります。
$Q3$.
次の曲線群における包絡線を求めなさい。
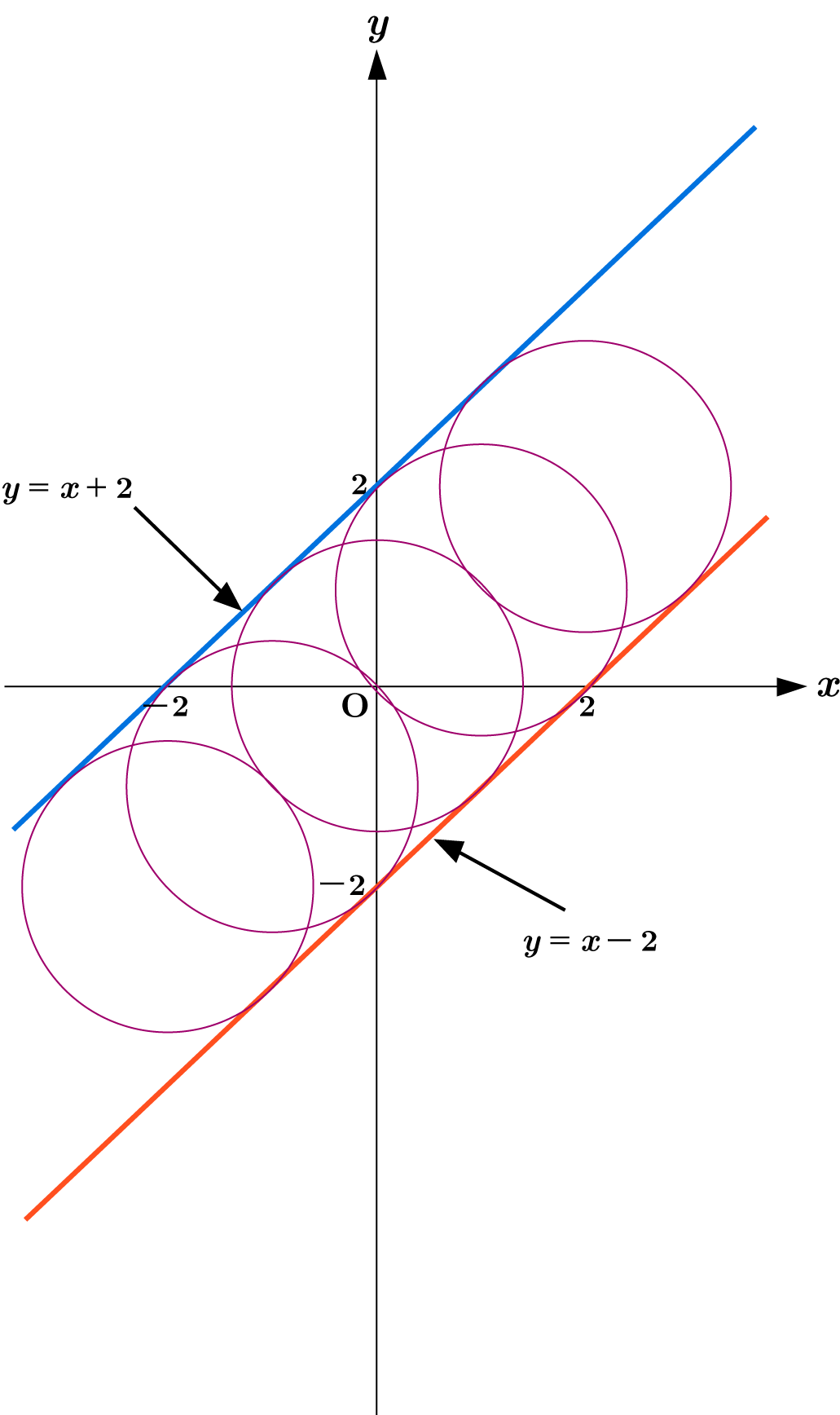
曲線群 $f(x,y,t) = (x-t)^2 + (y-t)^2 -2 = 0$
$y = x \pm 2$
$f(x,y,t) = (x-t)^2 + (y-t)^2 -2$ とすると
$f_t(x,y,t) = -2(x-t) - 2(y-2)$
より $f_t(x,y,t)=0$ とすると
$t = \dfrac{x+y}{2}$
$f(x,y,t)=0$ に代入すると
$\left( \dfrac{x-y}{2}\right)^2 + \left( \dfrac{-x+y}{2}\right)^2 - 2 =0$
整理すると $(y-x)^2 = 4$ となるので, 包絡線の方程式は
$y = x \pm 2$
となります。

媒介変数 $t$ を用いて $xy$ 平面上の曲線群が
$f(x,y,t) = 0$
で与えられている時, この曲線群の包絡線の方程式は $2$ つの方程式
$f(x,y,t)=0$
$f_t(x,y,t)=0$
から $t$ を消去することで得られます。
$f(x,y,t) = t^2x^2 + t -y$ とすると
$f_t(x,y,t) = 2tx^2 + 1$
より $f_t(x,y,t)=0$ とすると
$t = -\dfrac{1}{2x^2}$
元の曲線群の方程式に代入すると
$\left( -\dfrac{1}{2x^2}\right)^2x^2 - \dfrac{1}{2x^2} -y =0$
整理すると包絡線の方程式は
$y = -\dfrac{1}{4x^2}$
となります。