まず, $2$ つの曲線の交点を求めます。

$x^2-2 = -x^2+2x+2$

とすると

$2x^2 -2x -4 = 2(x+1)(x-2)=0$

よって交点の $x$ 座標は $x=-1,2$ となります。

$-1 \leqq x \leqq 2$ の区間では

$x^2 -2 \leqq -x^2 + 2x + 2$

であるので, 求める面積 $S$ は

$ $$\begin{eqnarray*} S &=& \int_{-1}^{2}\{(-x^2+2x+2)-(x^2-2)\}\ dx \\[1em] &=& \int_{-1}^{2}(-2x^2+2x+4)\ dx \\[1em] &=& \left[-\cfrac{2}{3}x^3+x^2+4x\right]_{-1}^2 \\[1em] &=& \left(-\cfrac{16}{3}+4+8\right)-\left(\cfrac{2}{3}+1-4\right) =9 \end{eqnarray*}$$ $

$\sqrt{x} = 2x$ とすると

$4x^2 - x = x(4x-1)=0$

よって交点の $x$ 座標は $x=0,\dfrac{1}{4}$ となります。

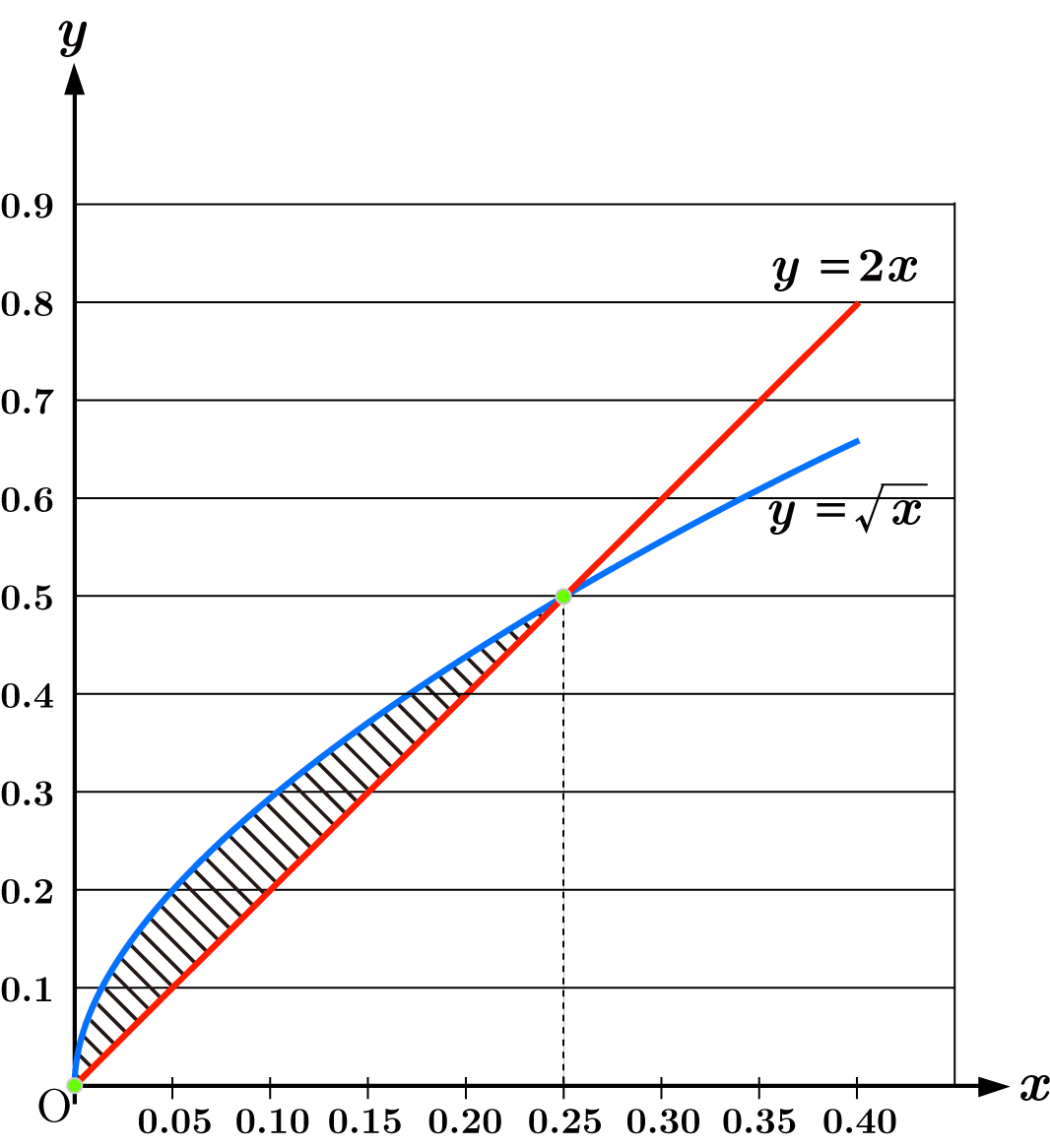
$0\leqq x \leqq \dfrac{1}{4}$ の区間では $2x \leqq \sqrt{x}$ であるので, 求める面積 $S$ は

$ $$\begin{eqnarray*} S &=& \int_{0}^{\frac{1}{4}}(\sqrt{x}-2x)\ dx \\[1em] &=& \left[\cfrac{2}{3} x^{\frac{3}{2}}-x^2 \right]_0^{\frac{1}{4}} \\[1em] &=& \cfrac{2}{3}\cdot \cfrac{1}{8}-\cfrac{1}{16} = \cfrac{1}{12}-\cfrac{1}{16} = \cfrac{1}{48} \end{eqnarray*}$$ $

まず $2$ つの接線の方程式を求めます。

$y' = 2x-1$ より, 点 $(2,2)$ における接線の傾きは $4-1=3$ であるから, 接線の方程式は

$y = 3(x-2)+2 = 3x-4$

となります。

同様に $(-4,20)$ における接線の傾きは $-8-1=-9$ であるから, 接線の方程式は

$y = -9(x+4) + 20 = -9x -16$

となります。

次に $2$ つの接線の交点を求めます。

$3x-4 = -9x-16$

とすると $12x = -12$ より $2$ つの接線の交点の $x$ 座標は $x=-1$ であることがわかります。

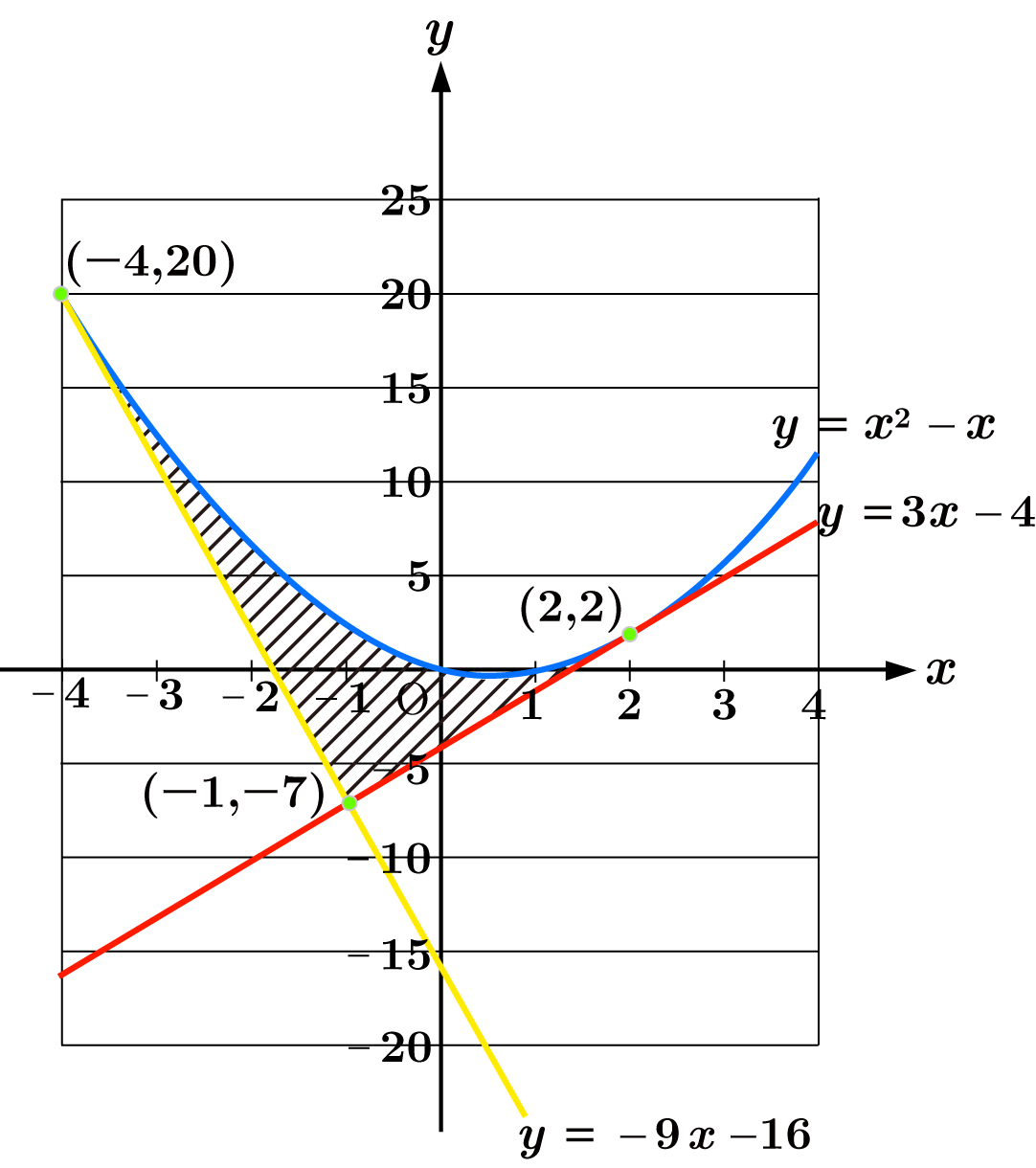
区間 $-4 \leqq x \leqq -1$ の部分の面積を考えると

$-9x -16 \leqq x^2 -x$

であるから, その面積 $S_1$ は

$ $$\begin{eqnarray*} S_1 &=& \int_{-4}^{-1}\{x^2-x-(-9x-16)\}\ dx \\[1em] &=& \int_{-4}^{-1}(x^2+8x+16)\ dx \\[1em] &=& \left[\cfrac{1}{3} x^3+4x^2+16x\right]_{-4}^{-1} \\[1em] &=& \left(-\cfrac{1}{3}+4-16\right)-\left(-\cfrac{64}{3}+64-64\right)=9 \end{eqnarray*}$$ $

また, $-1 \leqq x \leqq 2$ の部分の面積を考えると

$3x-4 \leqq x^2 -x$

であるから, その面積 $S_2$ は

$ $$\begin{eqnarray*} S_2 &=& \int_{-1}^{2}\{x^2-x-(3x-4)\}\ dx \\[1em] &=& \int_{-1}^{2}(x^2-4x+4)\ dx \\[1em] &=& \left[\cfrac{1}{3} x^3-2x^2+4x\right]_{-1}^2 \\[1em] &=& \left(\cfrac{8}{3}-8+8\right)-\left(-\cfrac{1}{3}-2-4\right) =9 \end{eqnarray*}$$ $

よって求める面積 $S$ は

$S= S_1+S_2 = 9+9=18$