$Q1$.
次の図形を $x$ 軸のまわりに回転してできる立体の体積 $V$ を求めなさい。
$Q2$.
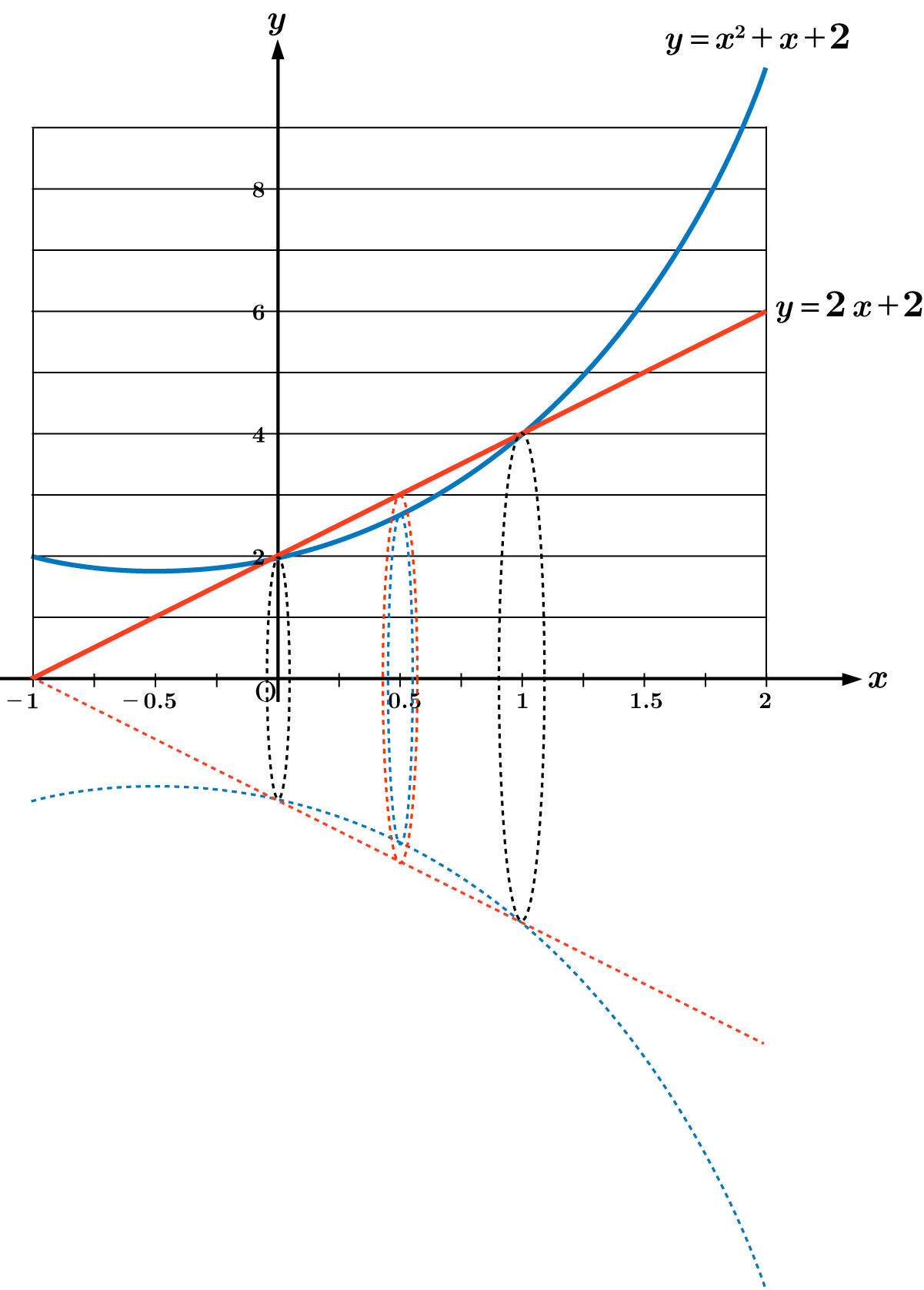
曲線 $y=x^2+x+2$ と直線 $y~2x+2$ で囲まれた図形を $x$ 軸のまわりに回転してできる立体の体積 $V$ を求めなさい。
最初に $2$ つの曲線の交点を求めましょう。
$x^2+x+2 = 2x+2$
とすると $x^2 -x= x(x-1)=0$ より $x=0,1$ となります。
積分区間は $0\leqq x \leqq 1$ であり, この区間では $x^2+x+2 \leqq 2x+2$ となります。
よって求める体積 $V$ は, 直線 $y=2x+2$ を $x$ 軸のまわりに回転してできる立体の体積 $V_1$ から, 曲線 $y=x^2+x+2$ を $x$ 軸のまわりに回転してできる立体の体積 $V_2$ を引いた値になります。
$\displaystyle V_1 = \int_0^1 \pi(2x+2)^2~dx$
であり, また
$\displaystyle V_2 = \int_0^1 \pi (x^2+x+2)^2 ~dx$
であるから求める体積 $V$ は
$\begin{eqnarray*} V & = & V_1 - V_2\\[0.5em] & = & \pi \int_0^1 (2x+2)^2 - (x^2+x+2)^2 ~ dx\\[1em] & = & \pi \int_0^1 (-x^4 - 2x^3 -x^2 + 4x)~dx\\[1em] & = & \pi \left[ -\dfrac{1}{5}x^5 -\dfrac{1}{2}x^4 - \dfrac{1}{3}x^3 +2x^2 \right]_0^1\\[1em] & = & \pi \left( -\dfrac{1}{5} - \dfrac{1}{2} - \dfrac{1}{3} + 2 \right) = \dfrac{29}{30}\pi \end{eqnarray*}$
$Q3$.
次の図形を $y$ 軸のまわりに回転してできる立体の体積 $V$ を求めなさい。
曲線 $x=g(y) ~(a\leqq y \leqq b)$ と $y$ 軸, 直線 $y=a$, $y=b$ で囲まれた領域を $y$ 軸のまわりに $1$ 回転させてできる立体の体積 $V$ は
$V = \displaystyle \int_a^b \pi \left\{ g(y) \right\}^2~dy$
で計算できます。
$y$ 軸のまわりに回転させるので $x \geqq 0$ としてよく, この時 $y=\dfrac{1}{2}x^2$ より
$x = \sqrt{2y}$
となります。よって求める回転体の体積 $V$ は
$\displaystyle V = \int_0^4 \pi (\sqrt{2y})^2~dy = \int_0^4 2\pi y~dy = \left[\pi y^2\right]_0^4 = 16\pi$
となります。
$Q4$.
曲線 $y=\sin x~(0 \leqq x \leqq \pi)$ と $x$ 軸で囲まれた図形を $x$ 軸のまわりに回転してできる立体の体積 $V$ を求めなさい。
$x$ 軸との交点の $x$ 座標は $x=0,\pi$ なので, 求める体積 $V$ は
$\begin{eqnarray*}V & = & \int_0^{\pi} \pi y^2 ~dx\\[1em] & = & \pi \int_0^{\pi} \sin^2 x ~dx\\[1em] &=& \dfrac{\pi }{2} \int_{0}^{\pi} (1 - \cos 2x)\ dx \\[1em] &=& \dfrac{\pi }{2} \left[x - \dfrac{1}{2} \sin 2x\right]_0^\pi = \dfrac{\pi ^2}{2} \end{eqnarray*}$

$Q5$.
曲線 $y=\sin x~(0 \leqq x \leqq \pi)$ と $x$ 軸で囲まれた図形を $y$ 軸のまわりに回転してできる立体の体積 $V$ を求めなさい。
$y= \sin x$ のグラフは $Q4$ のようになるので, 求める体積 $V$ は下図のように, 赤い部分を回転させたときの体積 $V_1$ から青い部分を回転させたときの体積 $V_2$ を引いた値になります。
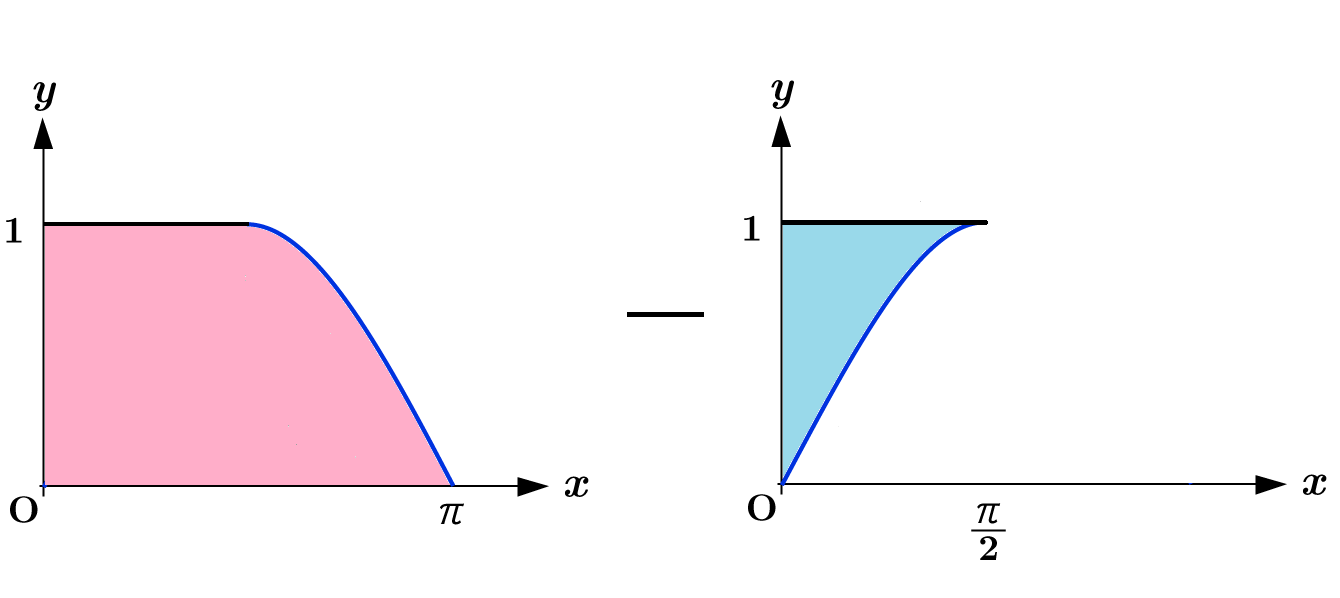
まず $V_1$ を求めると
$\displaystyle V_1 = \int_0^1 \pi x^2 ~dy$
となりますが, $y = \sin x$ より $dy = \cos x~dx$ であり
$y=0$ の時 $x=\pi$, $y=1$ の時 $x = \dfrac{\pi}{2}$
となるので
$\begin{eqnarray*}V_1 & = & \int_0^{1} \pi x^2 ~dy\\[1em] & = & \pi \int_{\pi}^{\frac{\pi}{2}} x^2 \cos x~dx = -\pi \int_{\frac{\pi}{2}}^{\pi} x^2 \cos x ~ dx \end{eqnarray*}$
となります。同様に $V_2$ を求めると
$\displaystyle V_2 = \int_0^1 \pi x^2 ~dy$
となりますが, この時は
$y=0$ の時 $x=0$, $y=1$ の時 $x = \dfrac{\pi}{2}$
となるので, $dy = \cos x ~dx$ より
$\displaystyle V_2 = \int_0^{1} \pi x^2 ~dy = \pi \int_{0}^{\frac{\pi}{2}} x^2 \cos x~dx$
以上から, 求める体積 $V$ は
$\begin{eqnarray*} V & = & V_1 - V_2\\[1em] & = & -\pi \int_{\frac{\pi}{2}}^{\pi} x^2 \cos x ~ dx - \pi \int_{0}^{\frac{\pi}{2}} x^2 \cos x~dx\\[1em] & = & -\pi \int_0^{\pi} x^2 \cos x~dx \end{eqnarray*}$
部分積分を $2$ 回行うと
$\begin{eqnarray*} V & = & -\pi \int_0^{\pi} x^2 \cos x~dx\\[1em] & = & -\pi\left( \left[ x^2 \sin x \right]_0^{\pi} - \int_0^{\pi}2x\sin x~dx \right)\\[1em] & = & -\pi \left(0 - \left[ -2x \cos x \right]_0^{\pi} + \int_0^{\pi} (-2\cos x) ~dx \right)\\[1em] & = & 2\pi^2 +2\pi \left[ \sin x \right]_0^{\pi} = 2\pi^2 \end{eqnarray*}$

曲線 $y=f(x) ~(a\leqq x \leqq b)$ と $x$ 軸, 直線 $x=a$, $x=b$ で囲まれた領域を $x$ 軸のまわりに $1$ 回転させてできる立体の体積 $V$ は
$V = \displaystyle \int_a^b \pi \left\{ f(x) \right\}^2~dx$
で計算できます。
曲線 $y=2\sqrt{x}$ は $x$ 軸と原点で交わるので, 求める体積 $V$ は
$\displaystyle V = \int_0^4 \pi (2\sqrt{x})^2~dx = \int_0^4 4\pi x~dx = \left[2\pi x^2\right]_0^4 = 32\pi$
となります。