平方完成して

$y = a(x-p)^2 +q$

の形にし, $a$ の符号と $q$ の値で判断します。

(1)
$x$ が実数の時, 常に $x^2 \geqq 0$ なので $y$ の値域は $y \geqq 0$ となります。

(2)
$x$ が実数の時, $x^2 \geqq 0$ なので $2x^2 \geqq 0$ です。

よって $y$ の値域は $y \geqq 0$ となります。

(3)
$x$ が実数の時, $x^2 \geqq 0$ なので $-3x^2 \leqq 0$ です。

よって $y$ の値域は $y \leqq 0$ となります。

(4)
$x^2 \geqq 0$ より $x^2 +3 \geqq 3$ です。

よって $y$ の値域は $y \geqq 3$ となります。

(5)
右辺を平方完成すると

$y = -(x-1)^2 + 1$

$(x-1)^2 \geqq 0$ より $-(x-1)^2 \leqq 0$ なので

$-(x-1)^2 +1 \leqq 1$

よって $y$ の値域は $y \leqq 1$ となります。

(6)
右辺を平方完成すると

$y = (x-2)^2 + 2$

ここで, $(x-2)^2 \geqq 0$ より

$(x-2)^2 +2 \geqq 2$

よって $y$ の値域は $y \geqq 2$ となります。

(1)
右辺を平方完成すると

$\begin{eqnarray*}y & = & 2(x-1)^2 +3\end{eqnarray*}$

$(x-1)^2 \geqq 0$ より

$2(x-1)^2 + 3 \geqq 3$

であり, 特に等号は $x=1$ の時のみ成り立ちます。

よって $y$ は $x=1$ の時, 最小値 $3$ を取り, 最大値は存在しません。

(2)

$\begin{eqnarray*}y & = & -(x-4)^2 +13\end{eqnarray*}$

であり, $(x-4)^2 \geqq 0$ より

$-(x-4)^2 \leqq 0$

よって

$-(x-4)^2 +13 \leqq 13$

等号は $x=4$ の時のみ成り立ちます。

以上から $y$ は $x=4$ の時, 最大値 $13$ を取り, 最小値は存在しません。

(1)
右辺を平方完成すると

$\begin{eqnarray*}y & = & (x+1)^2 - 4 ~~ (-4 \leqq x \leqq -2)\end{eqnarray*}$

このグラフを書くと図のようになります。

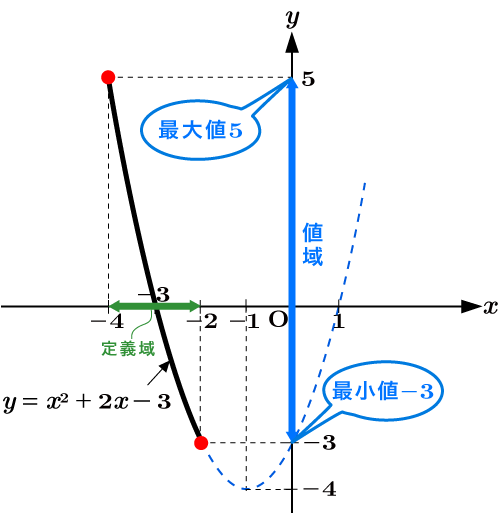
図より, $x=-4$ の時, 最大値 $y=5$ を取り, $x=-2$ の時, 最小値 $y=-3$ を取ることがわかります。

(2)
(1) と同様に

$\begin{eqnarray*}y & = & (x+1)^2 - 4 ~~ (-4 \leqq x \leqq 2)\end{eqnarray*}$

このグラフを書くと図のようになります。

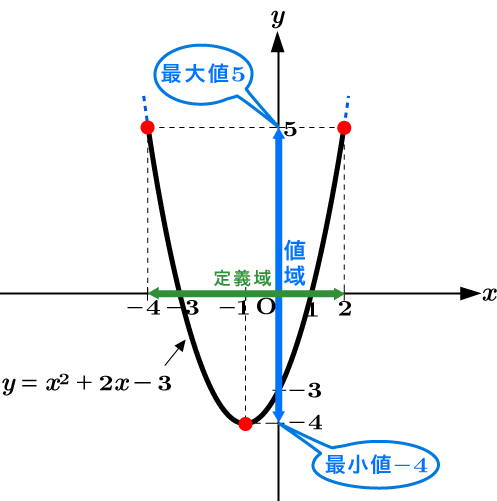
図より, $x=-4$ と $x=2$ の時, 最大値 $y=5$ を取り, $x=-1$ の時, 最小値 $y=-4$ を取ることがわかります。

(3)
右辺を平方完成すると

$\begin{eqnarray*}y & = & (x+4)^2 - 19 ~~ (-7 \leqq x \leqq -2)\end{eqnarray*}$

このグラフを書くと図のようになります。

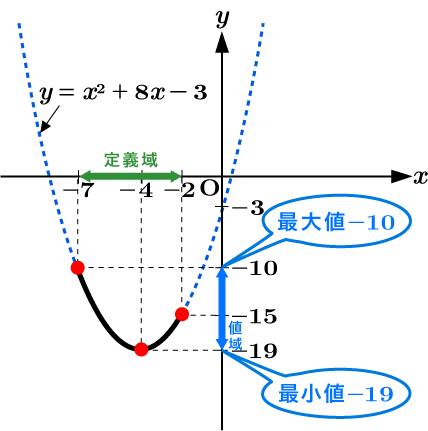
図より, $x=-7$ の時, 最大値 $y=-10$ を取り, $x=-4$ の時, 最小値 $y=-19$ を取ることがわかります。

単価を $x$ 円値上げすると販売個数は $2x$ 個下がるので, 単価が $(60+x)$ 円の時, この製品は $(300 -2x)$ 個売れることになります。

よって, 売上を $y$ とすると, 単価 $(60+x)$ 円の時の売上は

$\begin{eqnarray*}y & = & (60+x)(300-2x)\\[0.5em] & = & -2x^2 + 180x +18000\end{eqnarray*}$

となります。平方完成すると

$\begin{eqnarray*}y & = & -2(x-45)^2 + 22050\end{eqnarray*}$

よって $x=45$ の時, $y$ は最大値 $22050$ を取ることがわかります。

以上から, 単価 $60+45=105$ 円の時, 売上は最大となり, その時の金額は $22050$ 円になります。