$Q1$.
次の値を計算しなさい。
$Q2$.
$7$ 枚の異なるカードの中から $3$ 枚を選ぶ時, 選び方は何通りあるか答えなさい。
$7$ つのものの中から $3$ つを選ぶ組合せなので, その場合の数は
${}_7{\rm C}_3 = \dfrac{7\cdot 6\cdot 5}{3\cdot 2\cdot 1} = 35$
よって $35$ 通りになります。
$Q3$.
$9$ 枚のカードの次のように分ける時, 分け方は何通りあるか答えなさい。
(1)
$9$ 枚の異なるカードから $5$ 枚を選ぶ選び方は
${}_9{\rm C}_5 = \dfrac{9\cdot 8\cdot 7\cdot 6\cdot 5}{5\cdot 4\cdot 3\cdot 2\cdot 1} = 126$
より $126$ 通りになります。残りの $4$ 枚のカードから $3$ 枚を選ぶ選び方は
${}_4{\rm C}_3 = {}_4{\rm C}_1 = 4$
より $4$ 通りになります。よって積の法則から
$126 \cdot 4 = 504$
よってそのような分け方は全部で $504$ 通りになります。
(2)
$9$ 枚の異なるカードから $3$ 枚を選ぶ選び方は
${}_9{\rm C}_3 = \dfrac{9\cdot 8\cdot 7}{3\cdot 2\cdot 1} = 84$
より $84$ 通りになります。残りの $6$ 枚のカードから $3$ 枚を選ぶ選び方は
${}_6{\rm C}_3 = \dfrac{6\cdot 5\cdot 4}{3\cdot 2\cdot 1} = 20$
より $20$ 通りになります。
この $3$ つの組に分ける順番は考慮に入れないので, 求める場合の数は
$\dfrac{84\cdot 20}{3!} = 280$
より $280$ 通りになります。
$Q4$.
${\rm A}$, ${\rm B}$, ${\rm C}$, ${\rm D}$, ${\rm E}$, ${\rm F}$, ${\rm G}$ の $7$ 文字の中から $5$ 文字を選ぶ時, 次の条件を満たす選び方は何通りあるか答えなさい。
(1)
${\rm A}$ は常に選ばれるので, 残りの $6$ 文字から $4$ 文字を選べばよいことになります。よって
${}_6{\rm C}_4 = {}_6{\rm C}_2 = \dfrac{6\cdot 5}{2\cdot 1} = 15$
${\rm A}$ を選ぶ選び方は $15$ 通りになります。
【別解】:
$7$ 文字から $5$ 文字を選ぶ選び方は
${}_7{\rm C}_5 = {}_7{\rm C}_2 = \dfrac{7\cdot 6}{2\cdot 1} = 21$
より $21$ 通りになります。また, ${\rm A}$ が選ばれない選び方は, ${\rm A}$ 以外の $6$ 文字から $5$ 文字を選ぶ選び方なので
${}_6{\rm C}_5 = 6$
より $6$ 通りになります。
全ての場合の数 $21$ 通りから ${\rm A}$ を選ばない場合の数 $6$ 通りを引けば ${\rm A}$ を選ぶ場合の数になるので
$21-6=15$
より $15$ 通りになります。
(2)
${\rm A}$ は常に選ばれるので, 残りの $6$ 文字のうち ${\rm B}$ を除いた $5$ 文字から $4$ 文字を選べばよいから
${}_5{\rm C}_4 =5$
よって, そのような選び方は $5$ 通りになります。
$Q5$.
男子 $8$ 人と女子 $3$ 人の中から $4$ 人を選ぶ時, 女子が少なくとも $1$ 人選ばれる選び方は何通りあるか答えなさい。
全ての場合の数から, 女子が $1$ 人も選ばれない場合の数を引きましょう。
男子 $8$ 人と女子 $3$ 人の中から $4$ 人を選ぶ選び方は, $11$ 人から $4$ 人選ぶ選び方なので
${}_11{\rm C}_4 = \dfrac{11\cdot 10 \cdot 9\cdot 8}{4\cdot 3\cdot 2\cdot 1} = 330$
より $330$ 通りになります。
一方, 女子が $1$ 人も選ばれない選び方は, 男子 $8$ 人の中から $4$ 人を選ぶ選び方なので
${}_8{\rm C}_4 = \dfrac{8\cdot 7 \cdot 6\cdot 5}{4\cdot 3\cdot 2\cdot 1} = 70$
より $70$ 通りになります。
以上から, 女子が少なくとも $1$ 人選ばれる選び方は
$330 -70 = 260$
より $260$ 通りになります。
$Q6$.
男子 $8$ 人と女子 $4$ 人の中から $5$ 人の委員を選ぶとする。男子から $2$ 人, 女子から $3$ 人選ぶとき, 委員の選び方は何通りあるか答えなさい。
男子 $8$ 人の中から $2$ 人選ぶ選び方は
${}_8{\rm C}_2 = \dfrac{8\cdot 7}{2\cdot 1} = 28$
より $28$ 通りになります。また, 女子 $4$ 人の中から $3$ 人選ぶ選び方は
${}_4{\rm C}_3 = 4$
より $4$ 通りになります。よって求める場合の数は積の法則から
$28\cdot 4 = 112$
より $112$ 通りになります。
$Q7$.
正六角形の対角線は何本あるか答えなさい。
対角線は $6$ つの頂点から $2$ つの頂点を選べば作れるので, その $2$ 点の選び方は
${}_6{\rm C}_2 = \dfrac{6\cdot 5}{2\cdot 1} = 15$
より $15$ 通りになります。ただし, この $15$ 通りのうち $6$ 通りは正六角形の辺に対応するので
$15 - 6 =9$
よって正六角形の対角線は $9$ 本存在します。
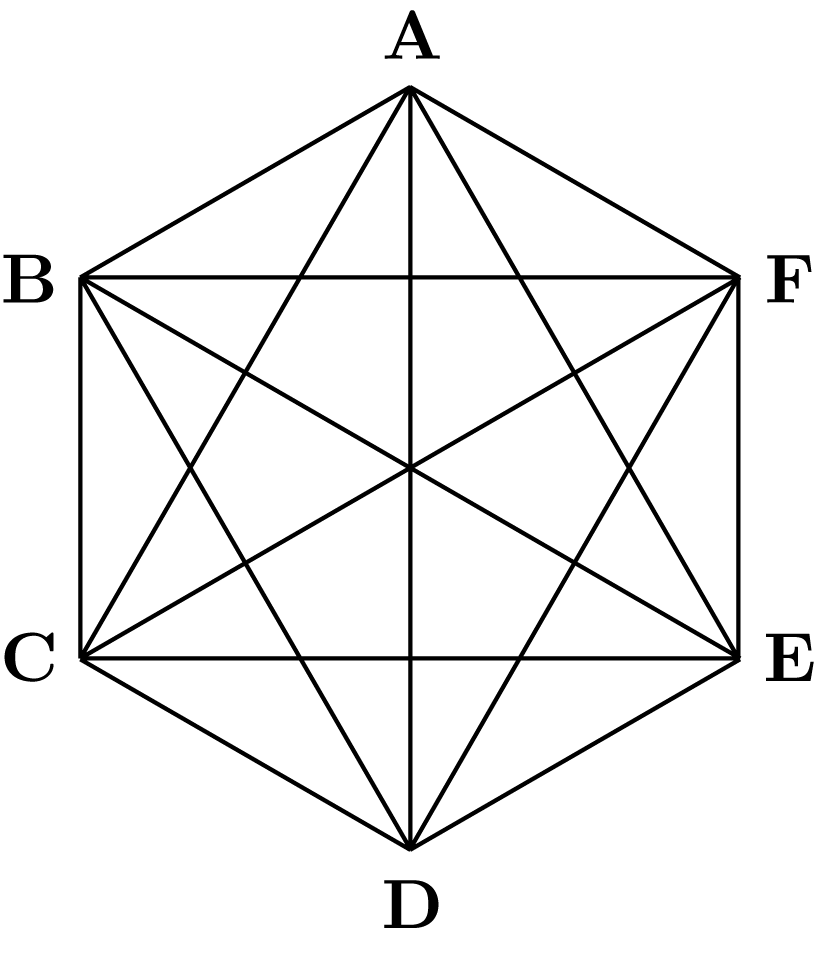
$Q8$.
正六角形の頂点を線で結んで三角形を作る時, 三角形はいくつできるか答えなさい。
$6$ つの頂点から $3$ つを選べば三角形が作れるので
${}_6{\rm C}_3 = \dfrac{6\cdot 5\cdot 4}{3\cdot 2\cdot 1} = 20$
よって三角形は $20$ 個作れます。

${}_n{\rm C}_r = \dfrac{ {}_n{\rm P}_r}{r!} = \dfrac{n(n-1)\cdots(n-r+1)}{r(r-1)\cdots 3\cdot 2\cdot1} = \dfrac{n!}{r!(n-r)!}$
となります。また, ${}_n{\rm C}_0 = 1$ であることに注意しましょう。
(1)
${}_4{\rm C}_1 = \dfrac{4}{1} = 4$
※ 一般に ${}_n{\rm C}_1 = n$ が成り立ちます。
(2)
${}_5{\rm C}_2 = \dfrac{5\cdot 4}{2\cdot 1} = 10$
(3)
${}_6{\rm C}_0 = 1$
※ ${}_n{\rm C}_0 = 1$ であることに注意しましょう。
(4)
${}_3{\rm C}_2 = \dfrac{3\cdot 2}{2\cdot 1} = 3$
(5)
${}_7{\rm C}_5 = {}_7{\rm C}_2 = \dfrac{7\cdot 6}{2\cdot 1} = 21$
(6)
${}_7{\rm C}_7 = {}_7{\rm C}_0 = 1$
※ 一般に ${}_n{\rm C}_r ={}_n{\rm C}_{n-r}$ が成り立ちます。(4), (5), (6) に適用して確認してみましょう。