$Q1$.
媒介変数 $t$ を用いて, 次の条件を満たす直線の媒介変数表示を求めなさい。
$Q2$.
以下の媒介変数表示された直線を $ax+by+c=0$ の形で表しなさい。
$2$ つの式から $t$ を消去して $x$ と $y$ の関係式にしましょう。
(1)
$\begin{eqnarray*} x &=& -2+3t& \cdots (1) \\[0.5em] y &=& 1+9t& \cdots (2) \end{eqnarray*}$
として $3\cdot (1) - (2)$ を考えると
$3x-y = -6 -1 = -7$
よってこの直線の方程式は $3x-y+7=0$ となります。
(2)
$\begin{eqnarray*} x &=& 3+2t& \cdots (1) \\[0.5em] y &=& -2-3t& \cdots (2) \end{eqnarray*}$
として, $3\cdot (1) + 2\cdot (2)$ を考えると
$3x+2y = 9-4=5$
よって直線の方程式は $3x+2y -5=0$ となります。
$Q3$ [補足].
$2$ つの直線 $x + 3y + 2 =0$, $2x+y+2=0$ のなす角 $\theta~\left( 0 \leqq \theta \leqq \dfrac{\pi}{2} \right)$ を求めなさい。
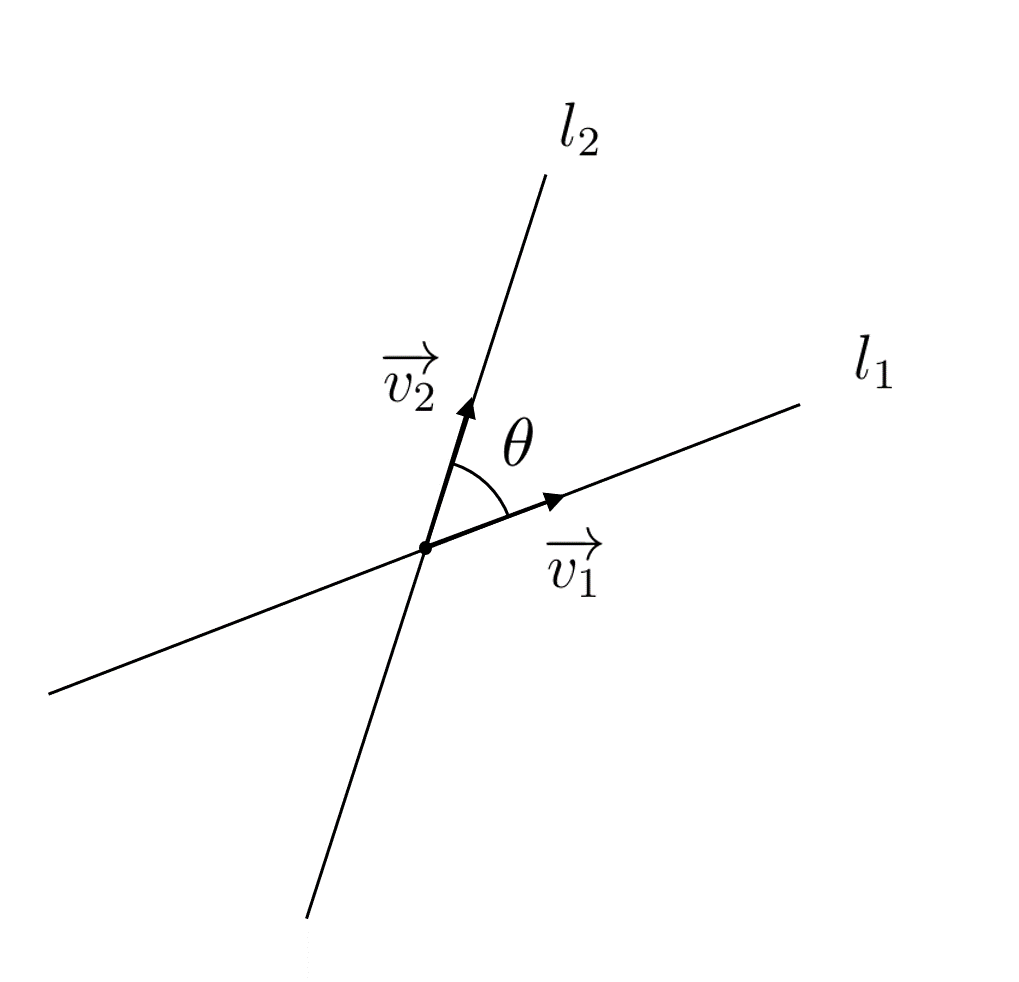
$2$ つの直線 $l_1$, $l_2$ の方向ベクトルを $\overrightarrow{v_1}$, $\overrightarrow{v_2}$ とし, $\overrightarrow{v_1}$ と $\overrightarrow{v_2}$ のなす角を $\theta$ とします。
ただし, ここで $0 \leqq \theta \leqq \dfrac{\pi}{2}$ となるように $\overrightarrow{v_1}$, $\overrightarrow{v_2}$ を選ぶものとします。
この時, この $\theta$ を $2$ 直線 $l_1$, $l_2$ のなす角 といいます。
直線 $x + 3y + 2 =0$ 上の点の位置ベクトルを $(x,y)$ とすると $y = -\dfrac{1}{3}x - \dfrac{2}{3}$ より
$(x,y) = \left(x~, -\dfrac{1}{3}x - \dfrac{2}{3}\right) = \left( 0~, -\dfrac{2}{3}\right) + \dfrac{1}{3}x(3,-1)$
よって $x + 3y + 2 =0$ は $(3,-1)$ を方向ベクトルに持つことがわかります。
同様に, 直線 $2x + y + 2=0$ 上に点の位置ベクトルを $(x,y)$ とすると $y = -2x -2$ より
$(x,y) = (x,-2x-2) = (0,-2) + x(1,-2)$
よって $2x + y + 2=0$ は $(1,-2)$ を方向ベクトルに持つことがわかります。
$2$ つのベクトル $(3,-1)$, $(1,-2)$ のなす角を $\theta$ とすると
$\cos \theta = \dfrac{(3,-1)\cdot (1,-2)}{|(3,-1)| |(1,-2)|} = \dfrac{3+2}{\sqrt{10}\sqrt{5}} = \dfrac{1}{\sqrt{2}}$
$0\leqq \theta \leqq \dfrac{\pi}{2}$ より $\theta = \dfrac{\pi}{4}$ となります。
$Q4$ [補足].
平面上の直線 $l$ に対し, $l$ の方向ベクトルと垂直なベクトルを $l$ の 法線ベクトル という。
直線 $l : ax + by+c=0$ に対し, ベクトル $(a,b)$ は $l$ の法線ベクトルであることを証明しなさい。
$b=0$ の時, $a\not=0$ であり直線の方程式は
$x= -\dfrac{c}{a}$
となりこれは $y$ 軸に平行な直線である。
一方, ベクトル $(a,0)$ は $y$ 軸に垂直なベクトルなので $(a,0)$ と $l$ は垂直である。
よって $(a,0)$ は $l$ の法線ベクトルである。
$b\not=0$ の時
$\begin{aligned} x &= -bt& \\ y &= - \dfrac{c}{b} +at \end{aligned}$
とすると $(x,y)$ は $ax+by+c=0$ を満たすので, これは $l$ の媒介変数表示である。
よって $(-b,a)$ は $l$ の方向ベクトルであるから, $(-b,a)$ と $(a,b)$ の内積を計算すると
$(-b,a)\cdot (a,b) = -ab + ab = 0$
$(a,b)$ と $(-b,a)$ は垂直なので, $(a,b)$ は $l$ の法線ベクトルである。
問題文にあるように, 直線 $l$ の方向ベクトルと垂直なベクトルをその直線の 法線ベクトル といいます。
方向ベクトルと同じように, 法線ベクトルは $1$ つではないことに注意しましょう。
$Q5$ [補足].
直線 $l : ax + by+c=0$ と $l$ 上にない点 ${\rm A}(x_0,y_0)$ に対し, 以下の問いに答えなさい。
(1)
$Q3$ よりベクトル $(a,b)$ は $l$ の法線ベクトルであり $l$ と $l'$ は垂直であるから, $l'$ は ${\rm A}(x_0,y_0)$ を通り $(a,b)$ に平行な直線であることがわかります。
よって $l'$ は媒介変数 $t$ を用いて
$\left\{ \begin{aligned} x &= x_0 + at \\ y &= y_0 + bt \end{aligned} \right.$
と表すことができます。
(2)
${\rm H}$ は $l'$ 上にあるので ${\rm H}$ の座標を $(x_0 + at,y_0+bt)$ とすると, ${\rm H}$ は $l$ 上にもあるので
$a(x_0+at) + b(y_0+bt) + c =0$
展開して整理すると
$t = -\dfrac{ax_0 + by_0 + c}{a^2 + b^2}$
となります。
$\overrightarrow{{\rm AH}} = (at,bt)$
であるから
$\begin{eqnarray*} |\overrightarrow{{\rm AH}}| & = & \sqrt{(at)^2 + (bt)^2}\\[1em] & = & |t|\sqrt{a^2 + b^2}\\[1em] & = & \left|-\dfrac{ax_0 + by_0 + c}{a^2 + b^2}\right| \sqrt{a^2 + b^2} = \dfrac{ |ax_0+by_0 +c|}{\sqrt{a^2+b^2}} \end{eqnarray*}$
よって $|\overrightarrow{{\rm AH}}| = \dfrac{ |ax_0 + by_0 + c|}{\sqrt{a^2 + b^2} }$ となります。
※補足
(2) で求めた $|\overrightarrow{{\rm AH}}|$ を, 点 ${\rm A}$ と直線 $l$ との距離といいます。
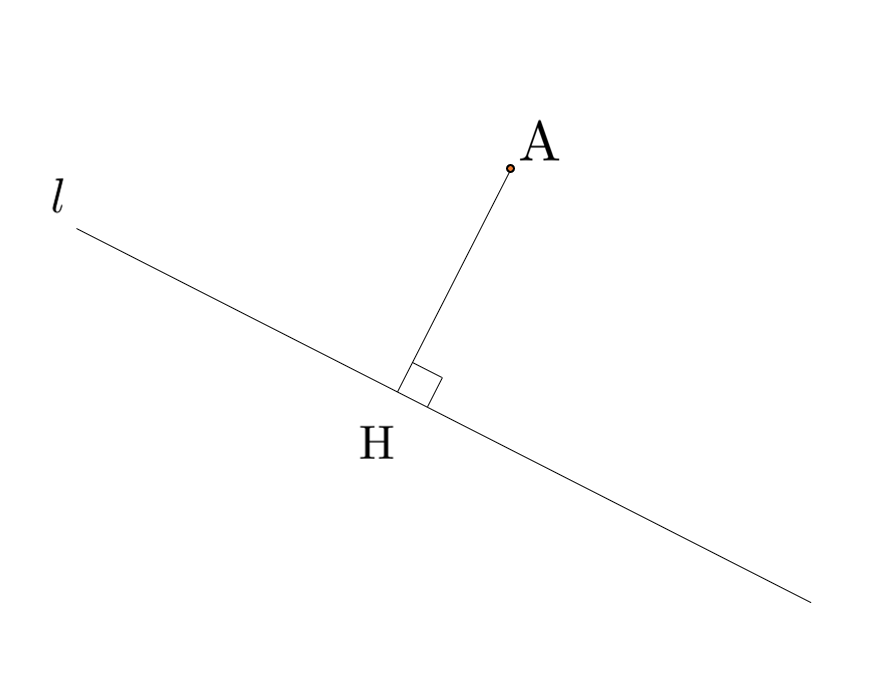
点 ${\rm A}(x_0,y_0)$ と直線 $l:ax+by+c=0$ との距離 $d$ は
$d = \dfrac{ |ax_0 + by_0 + c|}{\sqrt{a^2 + b^2} }$
で求めることができます。

(1)
点 $(x_0,y_0)$ を通り, 方向ベクトルが $(a,b)$ である直線の媒介変数表示は
$\begin{cases}x = x_0 + at\\y=y_0+bt \end{cases}$
となるので, 条件を満たす直線の媒介変数表示は
$\begin{cases}x = 6 + 3t\\y=5+7t \end{cases}$
となります。
(2)
条件を満たす直線の方向ベクトルは
$(-1,7) - (-4,-10) = (3,17)$
となるので, この直線は点 $(-4,-10)$ を通り, 方向ベクトルが $(3,17)$ である直線になります。
よって, その媒介変数表示は
$\begin{cases}x = -4 + 3t\\y=-10+17t \end{cases}$
となります。