導関数を求めると

$y' = 4x^3 + 24x^2 + 36x = 4x(x^2+6x+9) = 4x(x+3)^2$

よって $y'=0$ とすると, $x=-3,~0$ となります。また

$y'' = 12x^2 + 48x + 36 = 12(x+3)(x+1)$

よって $y''=0$ とすると, $x=-3,-1$ となります。

これらから増減表を作り, 曲線を描くと以下のようになります。

導関数を求めると

$y' = 1 - 2\cos x$

$0 \leqq x \leqq 2\pi$ であるから, $y'=0$ とすると, $x=\dfrac{\pi}{3},~\dfrac{5}{3}\pi$ となります。また

$y'' = 2\sin x$

$y''=0$ とすると, $x=0,~\pi,~2\pi$ となります。

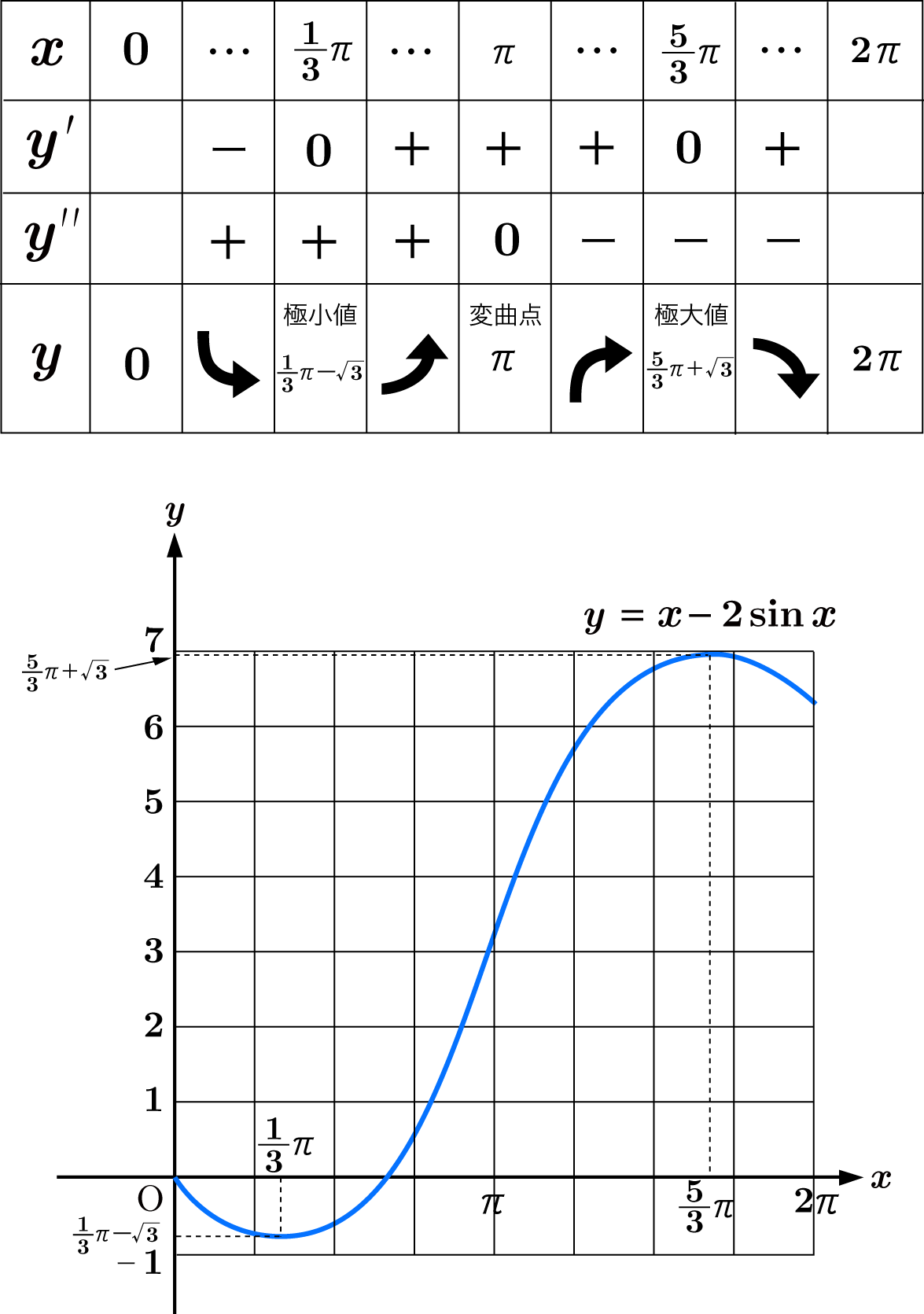
これらから増減表を作り, 曲線を描くと以下のようになります。

導関数を求めると

$y'=\left(-\dfrac{x^2}{2}\right)'e^{-\frac{x^2}{2}}=-xe^{-\frac{x^2}{2}}$

よって $y'=0$ とすると, $x=0$ となります。また

$y''= -e^{-\frac{x^2}{2}}-x\cdot \left(-xe^{-\frac{x^2}{2}} \right)=(x^2-1)e^{-\frac{x^2}{2}}=(x-1)(x+1)e^{-\frac{x^2}{2}}$

よって $y''=0$ とすると, $x=\pm 1$ となります。

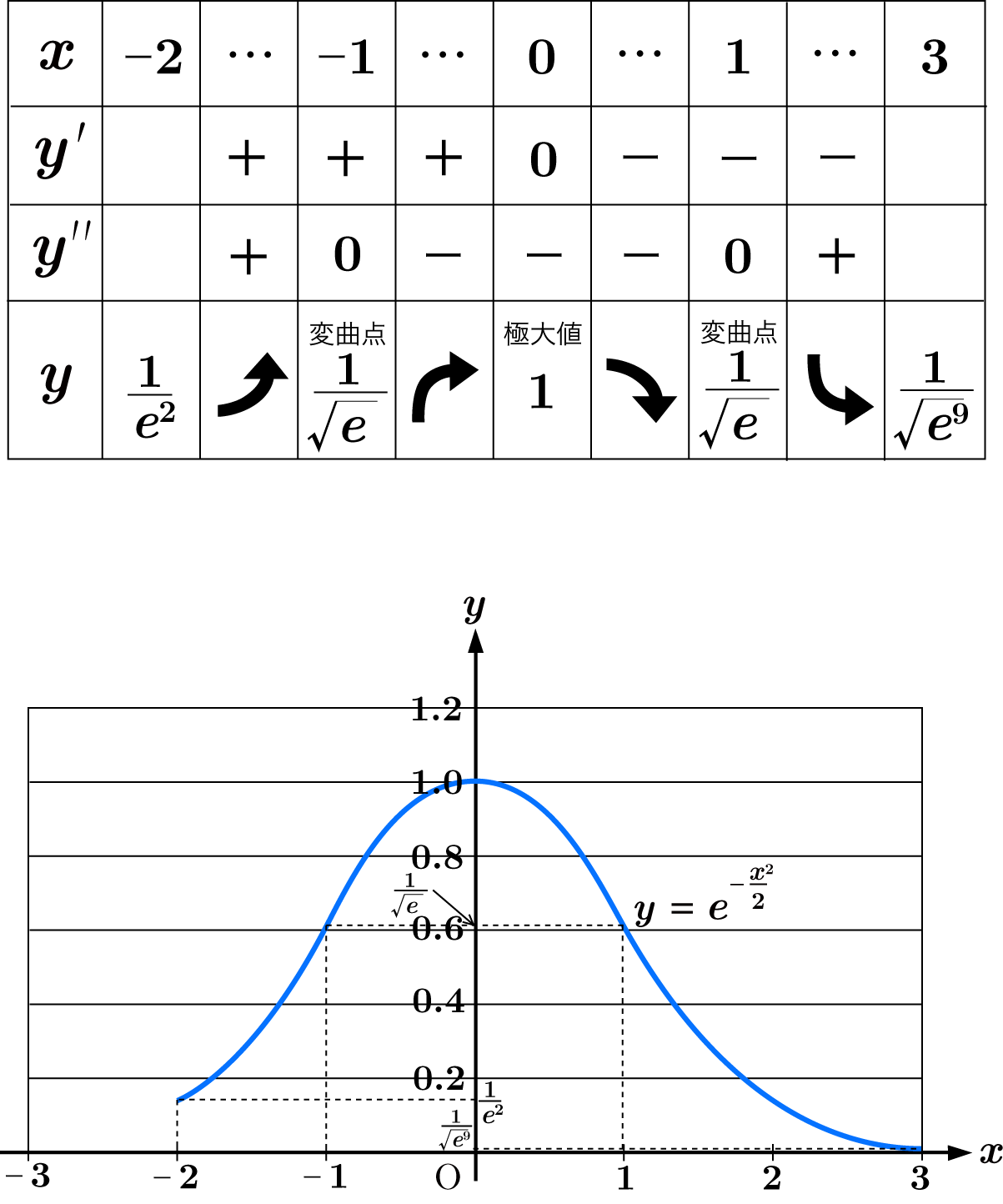
これらから増減表を作り, 曲線を描くと以下のようになります。

導関数を求めると

$y'=\sqrt{2-x^2}+x\cdot \dfrac{-2x}{2\sqrt{2-x^2}}=\dfrac{1-x^2}{\sqrt{2-x^2}}=\dfrac{(1-x)(1+x)}{\sqrt{2-x^2}}$

よって $y'=0$ とすると, $x=\pm 1$ となります。また

$y'=\dfrac{(1-x)(1+x)}{\sqrt{2-x^2}}=(1-x^2)(2-x^2)^{-\frac{1}{2}}$

であるから,

$ \begin{eqnarray*} y'' &=& -2x(2-x^2)^{-\frac{1}{2}}+(1-x^2)\cdot \left( -\cfrac{1}{2} \right)\cdot (-2x)\cdot (2-x^2)^{-\frac{3}{2}} \\[0.5em] &=& \left\{-2x(2-x^2)+x(1-x^2)\right\}(2-x^2)^{-\frac{3}{2}} \\[0.5em] &=& x(x^2-3)(2-x^2)^{-\frac{3}{2}} \end{eqnarray*} $

よって $y''=0$ とすると, $x=0,\pm\sqrt{3}$ となります。

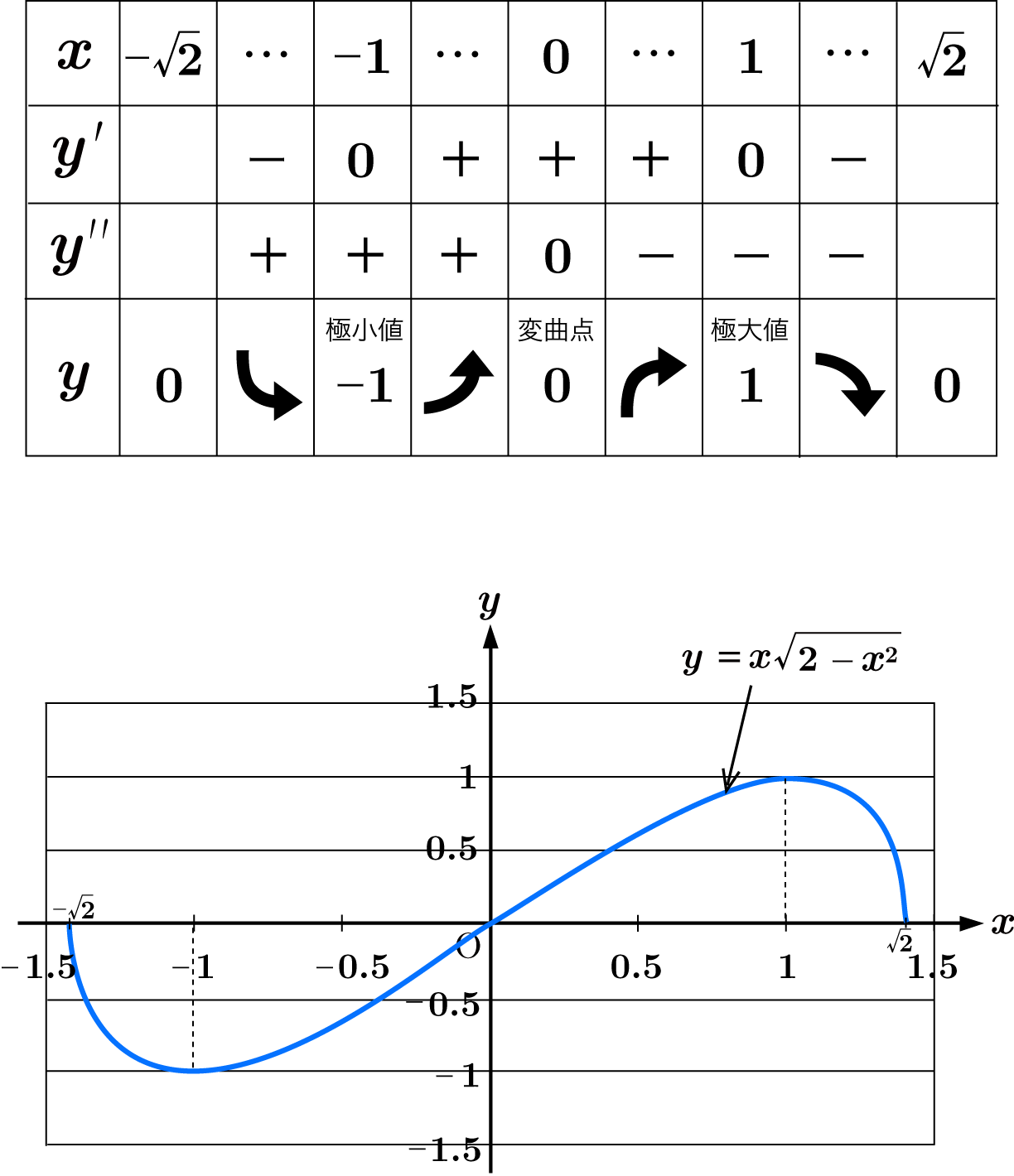
これらから増減表を作り, 曲線を描くと以下のようになります。