$Q1$.
次の関数の最大値と最小値を求めなさい。
解答・解説を見る$Q2$.
次の関数の最大値と最小値を求めなさい。
解答・解説を見る(1)
$f'(x) = \dfrac{2x-4}{2\sqrt{x^2 -4x + 8}} = \dfrac{x-2}{\sqrt{x^2 - 4x + 8}}$
であるから $f'(x) = 0$ の時, $x=2$ となります。
$ x−9 ⋯ 2 ⋯ 3f′(x)−0+f(x)5√5↘2↗√5 $
増減表から
$x=2$ の時, 最小値 $2$
を取り, また
$x=-9$ の時, 最大値 $5\sqrt{5}$
を取ることがわかります。
(2)
$f'(x) = -\dfrac{\sin x}{2\sqrt{5+\cos x}}$
であるから $f'(x) = 0$ とすると
$\sin x= 0$
$0\leqq x \leqq 2\pi$ より, $f'(x)=0$ の時, $x=0,~\pi,~2\pi$ となります。
$ x0 ⋯ π ⋯ 2πf′(x)0−0+0f(x)√6↘2↗√6 $
増減表から
$x=\pi$ の時, 最小値 $2$
を取り, また
$x=0$ または $x=2\pi$ の時, 最大値 $\sqrt{6}$
を取ることがわかります。
$Q3$.
$x \geqq 0$ の時, $f(x) = x^3 + 3x^2 -9x + 12 \gt 0$ であることを証明しなさい。
解答・解説を見る$f(x)$ を微分すると
$f'(x)= 3x^2 + 6x -9 = 3(x+3)(x-1)$
$x\geqq 0$ であるから, $f'(x)=0$ とすると $x=1$ である。
よって増減表は以下のようになる。
$ x0 ⋯ 1 ⋯ f′(x)−0+f(x)12↘7↗ $
$f(x)$ は $x=1$ で最小値 $7$ を取るので, $x \geqq 0$ の時 $f (x) \gt 0$ である。
$Q4$.
次の方程式が $3$ つの異なる実数解を持つような実数 $a$ の範囲を求めなさい。
解答・解説を見る$x^3 + 6x^2+9x+7 = -a$ より
$f(x) = x^3 + 6x^2 + 9x + 7$
として曲線 $y = f(x)$ と直線 $y = -a$ が $3$ つの共有点を持つような $a$ の範囲を求めればよいことになります。
$f(x)$ を微分すると
$f'(x) = 3x^2 + 12x + 9 = 3(x+3)(x+1)$
よって $f'(x) = 0$ とすると $x=-3,-1$ となります。
$ x ⋯ −3 ⋯ −1 ⋯ f′(x)+0−0+f(x)↗7↘3↗ $
増減表から, 関数 $y=f(x)$ のグラフは以下のようになります。
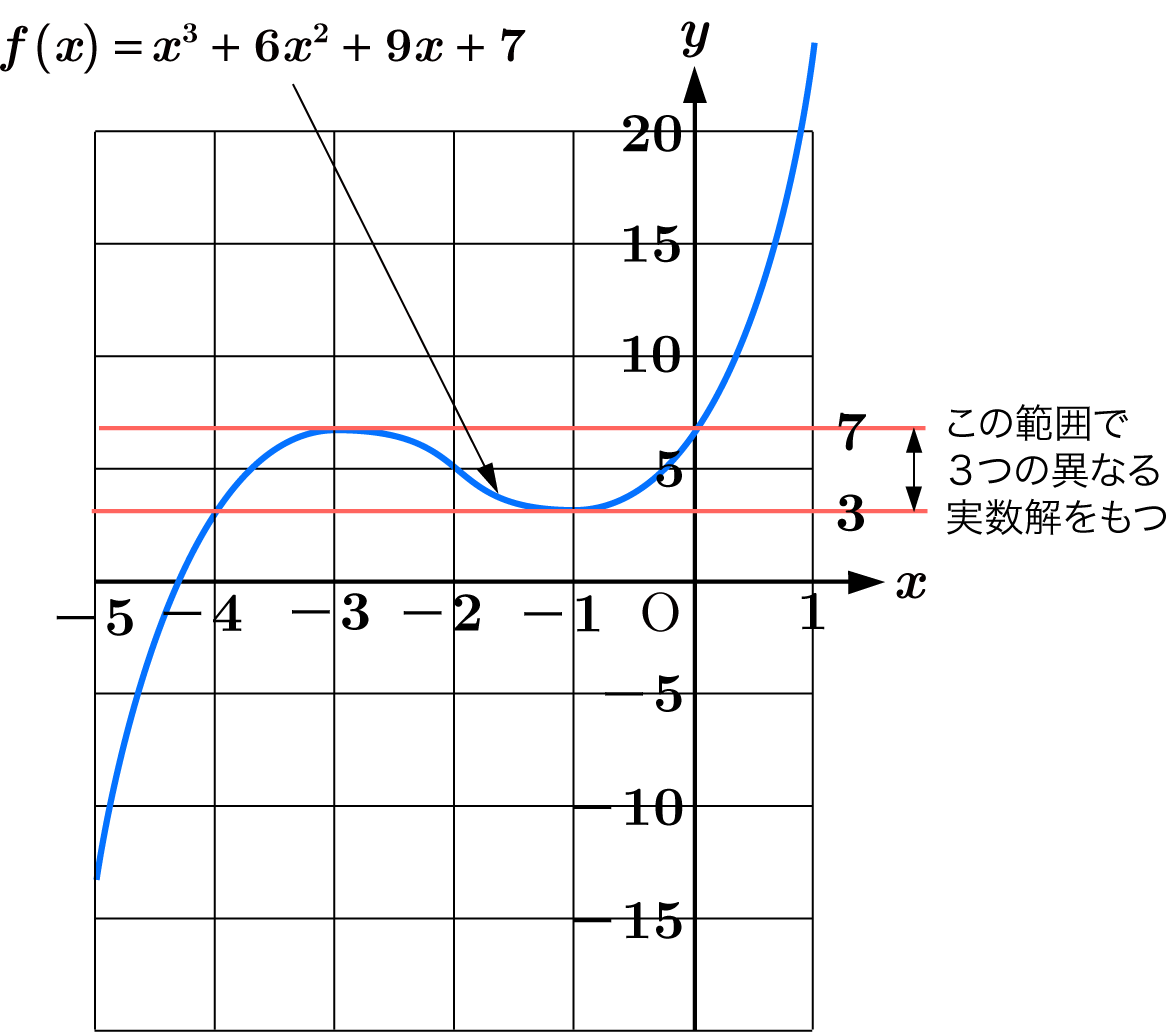
グラフから, $3 \lt -a \lt 7$ の時, 曲線 $y=f(x)$ と直線 $y=-a$ は共有点を $3$ つ持つことがわかります。
よって方程式が異なる $3$ つの実数解を持つような $a$ の範囲は
$-7 \lt a \lt -3$
となります。
(1)
$f'(x) = 3x^2 - 6x+9 = 3(x+1)(x-3)$
であるから $f'(x) = 0$ の時, $x=-1,~3$ となります。
$ x−4 ⋯ −1 ⋯ 3 ⋯ 6f′(x)+0−0+f(x)−73↗8↘−24↗57 $
増減表から
$x=-4$ の時, 最小値 $-73$
を取り, また
$x=6$ の時, 最大値 $57$
を取ることがわかります。
(2)
$f(x) = \dfrac{5(x^2+9) - 90}{x^2+9} = 5 - \dfrac{90}{x^2+9}$
であるから
$f'(x) = \dfrac{180x}{(x^2+9)^2}$
よって $f'(x)=0$ の時, $x=0$ となります。
$ x−1 ⋯ 0 ⋯ 3f′(x)−0+f(x)−4↘−5↗0 $
増減表から
$x=0$ の時, 最小値 $-5$
を取り, また
$x=3$ の時, 最大値 $0$
を取ることがわかります。