$Q1$.
次の不等式を解きなさい。
解答・解説を見る$Q2$.
$1$ 個 $100$ 円の商品 ${\rm A}$ と, $1$ 個 $80$ 円の商品 ${\rm B}$ があり, ${\rm A}$ と ${\rm B}$ を合計で $8$ 個買いたいとする。
合計金額を $720$ 円以下にしたい時に ${\rm A}$ は最大でいくつ買えるか答えなさい。
解答・解説を見る商品 ${\rm A}$ を $x$ 個買うとすると, ${\rm B}$ を $(8-x)$ 個買うことになります。この時, 合計金額は
$100x + 80(8-x) = 20x+640$
となります。これを $720$ 円以下にしたいので
$20x+640 \leqq 720$
$640$ を右辺に移項し, 両辺を $20$ で割ると
$x \leqq 4$
購入できる ${\rm A}$ の数は $4$ 個以下であるので, 最大で $4$ 個買えることがわかります。
$Q3$.
次の連立不等式を解きなさい。
解答・解説を見る全ての不等式を同時に満たす範囲が解になります。
$2x+19 \gt 3$ の $19$ を移項し, 両辺を $2$ で割ると
$x \gt -8$
また, $3x+18 \lt 9$ の $18$ を移項し, 両辺を $3$ で割ると
$x \lt -3$
解はこれらを同時に満たす範囲なので $-8 \lt x \lt -3$ が解となります。
$Q4$.
次の不等式を解きなさい。
解答・解説を見る(1)
$x$ の値に対する, 各因数の符号は下図になります。
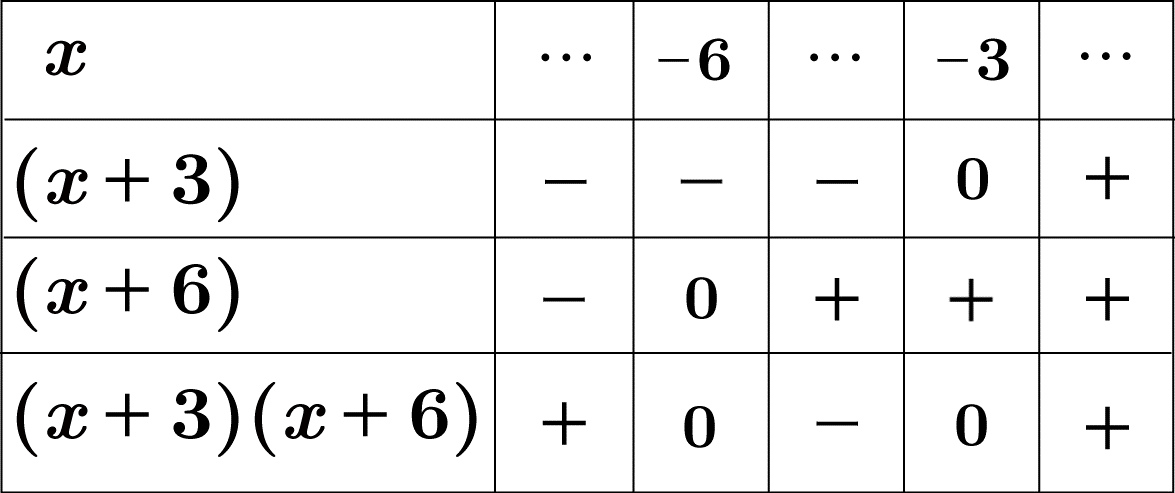
$(x+3)(x+6) \gt 0$ なので, この図から $x \lt -6$, $-3 \lt x$ が解となります。
(2)
左辺を因数分解すると
$x^2 + x -30 = (x+6)(x-5)$
$x$ の値に対する各因数の符号は下図になります。
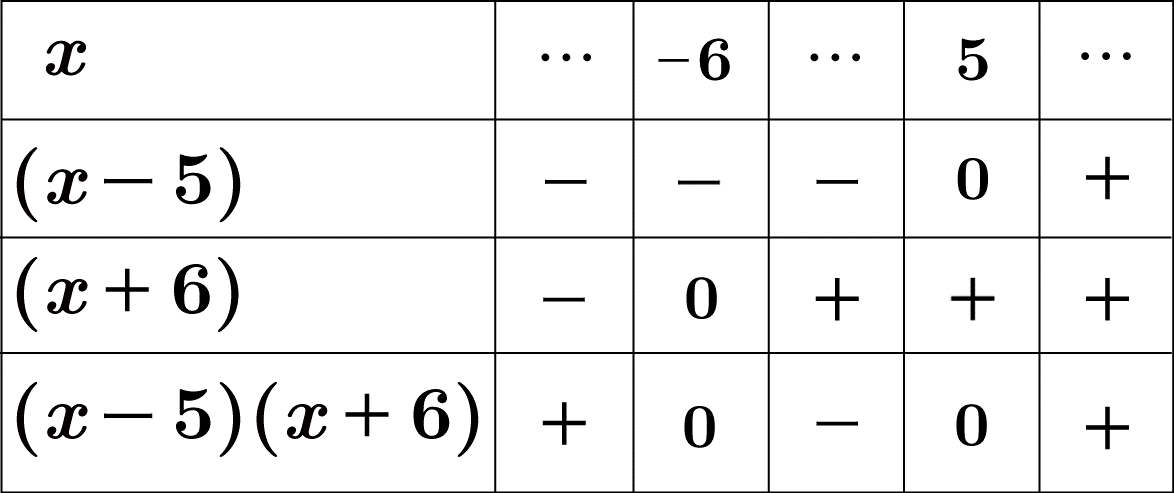
$x^2 + x -30 \gt 0$ なので, この図から $-6 \leqq x \leqq 5$ が解となります。
(3)
$x$ の値に対する, 各因数の符号は下図になります。
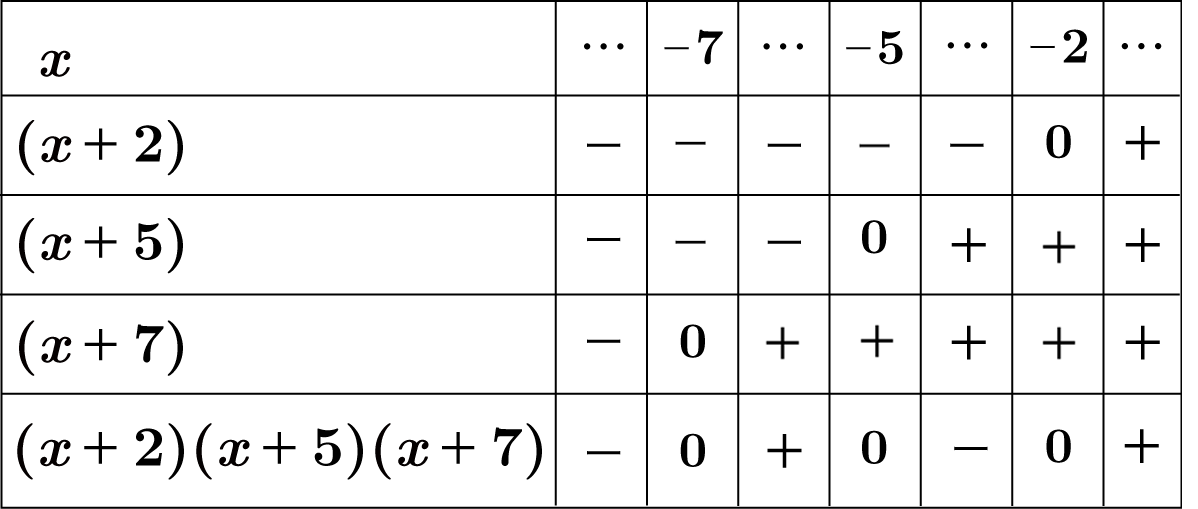
$(x+2)(x+5)(x+7) \gt 0$ なので, $-7 \lt x \lt -5$, $-2 \lt x$ が解となります。
(4)
$f(x) = x^3 -2x^2 -21x -18$
とおくと, $f(-1)=-1-2+21-18=0$ であるから, 因数定理より $f(x)$ は $(x+1)$ を因数に持ちます。よって
$\begin{eqnarray*}f(x) & = & (x+1)(x^2-3x-18)\\[0.5em] & = & (x+1)(x+3)(x-6)\end{eqnarray*}$
よって与えられた不等式は
$(x+3)(x+1)(x-6) \leqq 0$
と表すことができます。
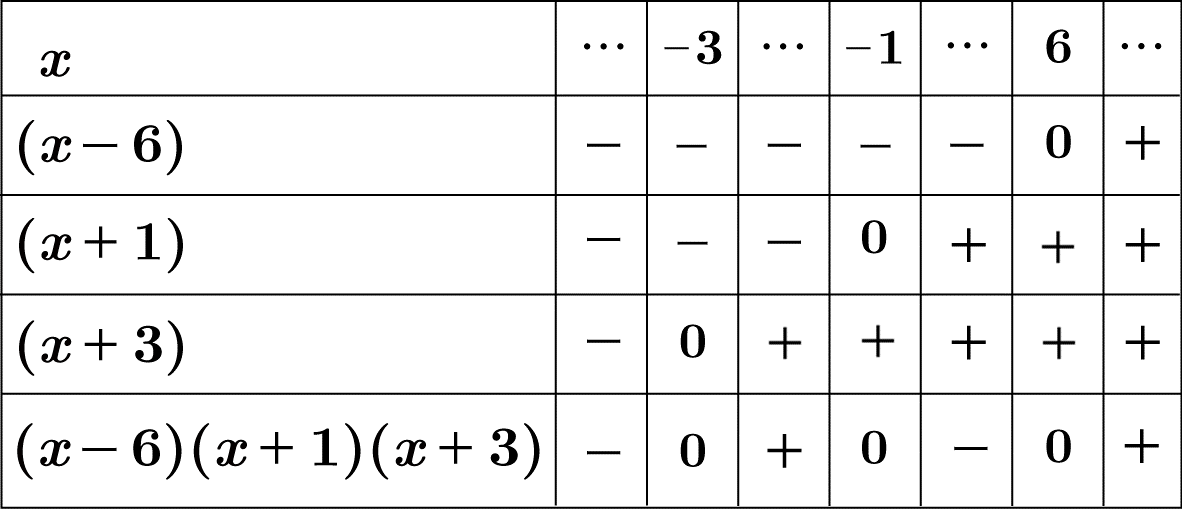
上図から $x \leqq -3$, $-1 \leqq x \leqq 6$ が解となります。
$Q5$.
$x \gt 0$ の時, $x + \dfrac{4}{x} \geqq 4$ が成り立つことを示しなさい。
解答・解説を見る$x \gt 0$ ならば $\dfrac{4}{x} \gt 0$ なので, 相加相乗平均の関係から
$x + \dfrac{4}{x} \geqq 2\sqrt{x \cdot \dfrac{4}{x} } = 4$
よって, $x \gt 0$ の時, $x + \dfrac{4}{x} \geqq 4$ が成り立つ。
また等号は $x = \dfrac{4}{x}$ の時, すなわち $x=2$ の時かつその時のみ成り立つ。
$Q6$.
任意の $a$, $b$, $c$, $d$ に対し, $(a^2 + b^2)(c^2 + d^2) \geqq (ac+bd)^2$ が成り立つことを示しなさい。
解答・解説を見る左辺 $-$ 右辺 を考えると
$\begin{eqnarray*}(a^2 + b^2)(c^2+ d^2) - (ac+bd)^2 & = & (a^2c^2 + a^2d^2 + b^2c^2 + b^2d^2) - (a^2c^2 + 2abcd + b^2d^2)\\[0.5em] & = & a^2d^2 - 2abcd + b^2d^2\\[0.5em] & = & (ad -bc)^2\end{eqnarray*}$
$(ad-bc)^2 \geqq 0$ より
$(a^2 + b^2)(c^2+ d^2) - (ac+bd)^2 \geqq 0$
よって $(a^2 + b^2)(c^2+ d^2) \geqq (ac+bd)^2$ が成り立つ。
また等号は $ad-bc=0$, すなわち $ad=bc$ の時かつその時のみ成り立つ。
(1)
$2x$ を左辺に, $5$ を右辺に移項すると
$\begin{eqnarray*}4x-2x & \gt & 7-5\\[0.5em] 2x & \gt & 2\end{eqnarray*}$
両辺を $2$ で割れば $x \gt 1$ となります。
(2)
$2x$ を左辺に, $-4$ を右辺に移項すると
$\begin{eqnarray*}-2x -2x & \gt & 8+4\\[0.5em] -4x & \gt & 12\end{eqnarray*}$
両辺を $-3$ で割れば $x \lt -3$ となります。