(1)
$\cos \theta = \dfrac{\sqrt{2}}{2}$ となるのは $\theta = \dfrac{\pi}{4} + 2n\pi$ の時と, $\theta = \dfrac{7}{4}\pi + 2n\pi$ ($n$ は整数) の時です。

$0 \leqq \theta \lt 2\pi$ より, $\theta = \dfrac{\pi}{4}$ と $\theta = \dfrac{7}{4}\pi$ が解となります。

(2)
$\sin \theta = \dfrac{1}{2}$ となるのは $\theta = \dfrac{\pi}{6} + 2n\pi$ の時と, $\theta = \dfrac{5}{6}\pi + 2n\pi$ ($n$ は整数) の時です。

$0 \leqq \theta \lt 2\pi$ より, $\theta = \dfrac{\pi}{6}$ と $\theta = \dfrac{5}{6}\pi$ が解となります。

(3)
$\tan \theta = -\dfrac{\sqrt{3}}{3}$ となるのは $\theta = \dfrac{5}{6}\pi + n\pi$ ($n$ は整数) の時です。

$0 \leqq \theta \lt 2\pi$ より, $\theta = \dfrac{5}{6}\pi$ と $\theta = \dfrac{11}{6}\pi$ が解となります。

(1)
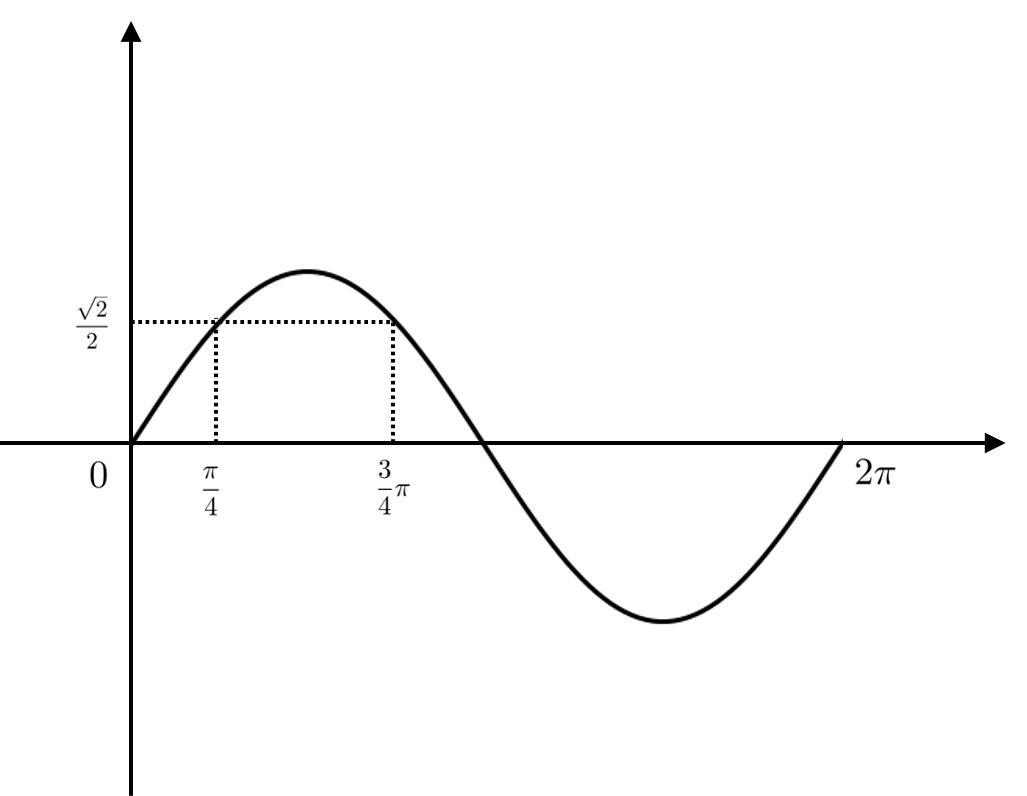
$\sin \theta = \dfrac{\sqrt{2}}{2}$ の時, $\theta = \dfrac{\pi}{4}$ または $\dfrac{3}{4}\pi$ となります。

下のグラフから $\sin \theta \gt \dfrac{\sqrt{2}}{2}$ となるのは $\dfrac{\pi}{4} \lt \theta \lt \dfrac{3}{4}\pi$ の時です。

(2)
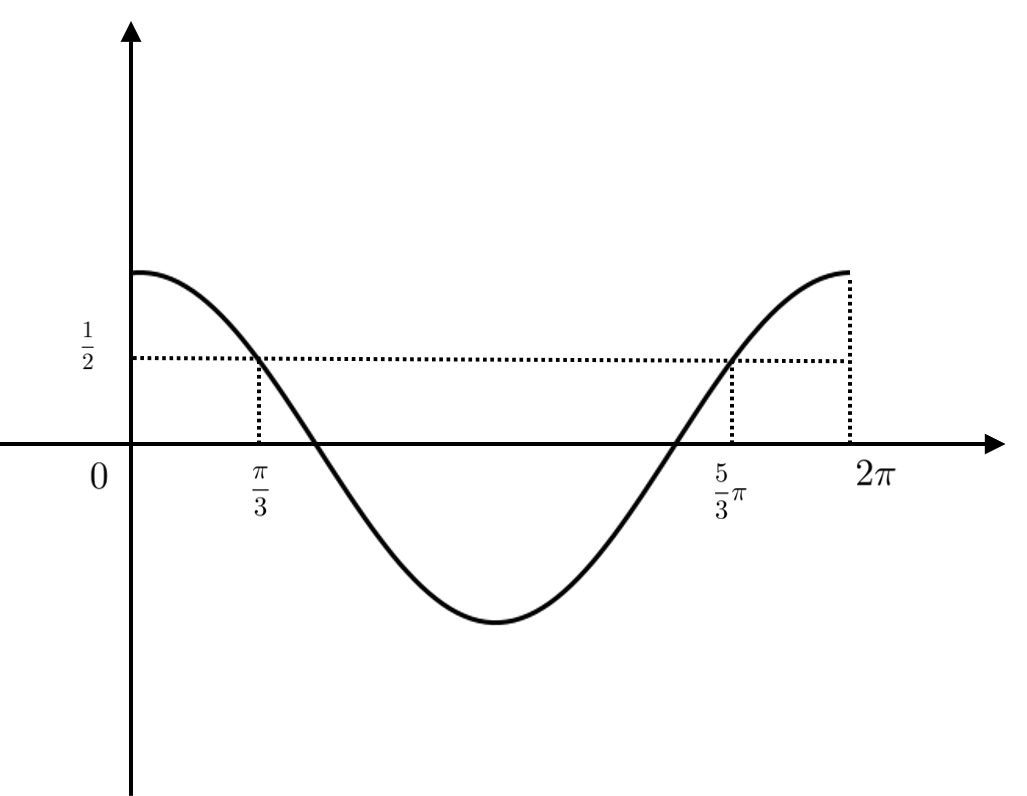
$\cos \theta = \dfrac{1}{2}$ の時, $\theta = \dfrac{\pi}{3}$ または $\dfrac{5}{3}\pi$ となります。

$0 \leqq \theta \lt 2\pi$ より, 下のグラフから $\cos \theta \gt \dfrac{1}{2}$ となるのは $0 \leqq \theta \lt \dfrac{\pi}{3}$ または $\dfrac{5}{3}\pi \lt \theta \lt 2\pi$ の時です。

(3)
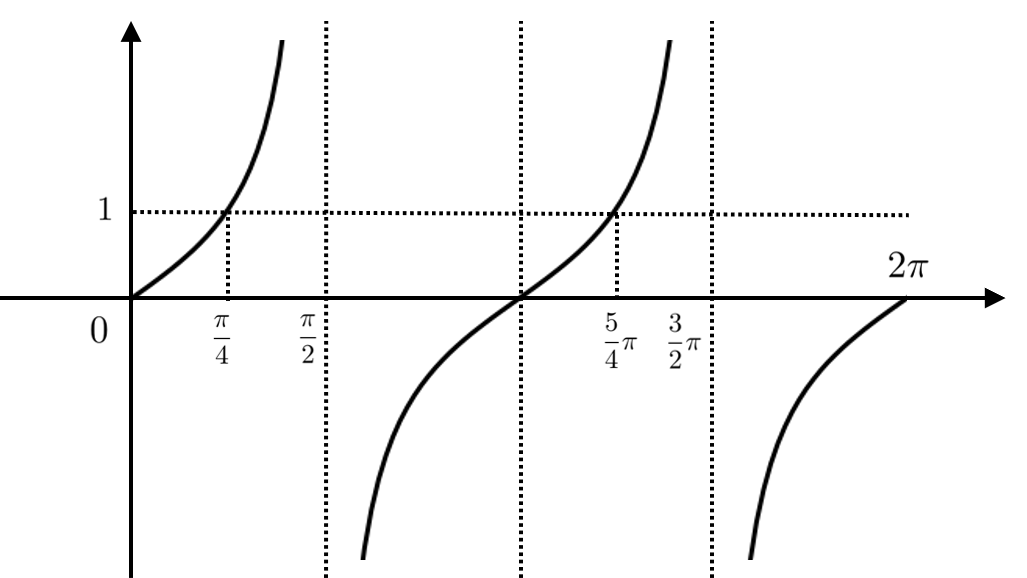
$\tan \theta = 1$ の時, $\theta = \dfrac{\pi}{4}$ または $\dfrac{5}{4}\pi$ となります。

下のグラフから $\tan \theta \geqq 1$ となるのは $\dfrac{\pi}{4} \leqq \theta \lt \dfrac{\pi}{2}$ または $\dfrac{5}{4}\pi \leqq \theta \lt \dfrac{3}{2}\pi$ の時です。

関数 $y=f(x)$ について, 全ての $x$ に対して

$f(x+p) = f(x)$

となるような最小の正の数 $p$ を, この関数の 周期 といいます。

(1)
$f(x) = \dfrac{1}{3}\sin 2x$ とすると, $y = \sin x$ の周期は $2\pi$ であるから

$f(x + \pi) = \dfrac{1}{3}\sin2(x+\pi) = \dfrac{1}{3}\sin \left( 2x + 2\pi \right) = \dfrac{1}{3}\sin 2x = f(x)$

よって $y =\dfrac{1}{3}\sin 2x$ の周期は $\pi$ となります。

(2)
$f(x) = 2\cos \left( \dfrac{1}{2}x - \pi \right)$ とすると, $y = \cos x$ の周期が $2\pi$ であるから

$f(x + 4\pi) = 2\cos\left( \dfrac{1}{2}(x+4\pi) - \pi \right) = 2\cos \left( \left(\dfrac{1}{2}x - \pi\right) + 2\pi \right) = 2\cos \left( \dfrac{1}{2}x - \pi \right) = f(x)$

よって $y = 2\cos \left( \dfrac{1}{2}x - \pi \right)$ の周期は $4\pi$ となります。

(3)
$f(x) = \tan \pi x$ とすると, $y =\tan x$ の周期は $\pi$ であるから

$f(x+1)= \tan \pi(x+1) = \tan \left( \pi x + \pi \right) = \tan \pi x = f(x)$

よって, $y = \tan \pi x$ の周期は $1$ となります。