$Q1$.
あるお店ではショートケーキを $100$ 個作るには「卵」$2 ~{\rm kg}$, 「砂糖」$1~{\rm kg}$ 必要であり, フルーツケーキを $100$ 個作るには「卵」$1 ~{\rm kg}$, 「砂糖」$2~{\rm kg}$ 必要である。
また, ショートケーキ $100$ 個の売上は $5$ 万円, フルーツケーキ $100$ 個の売上は $7$ 万円である。
この時, 「卵」$9~{\rm kg}$ 以内, 「砂糖」$9~{\rm kg}$ 以内として売上をできるだけ多くするには, ショートケーキとフルーツケーキを何個づつ作ればよいか。
また, その時の売上を求めなさい。ただし, 作ったケーキは全て売れるものとする。
$Q2$.
あるお好み焼き屋では関西風と広島風のお好み焼きによって価格が違っており, 広島風のお好み焼きが $400$ 円, 関西風のお好み焼きが $500$ 円 である。
また, 広島風のお好み焼きは小麦粉 $400~{\rm g}$, キャベツ $100~{\rm g}$ 必要であり, 関西風のお好み焼きは小麦粉 $100~{\rm g}$, キャベツ $300~{\rm g}$ 必要である。
使用する小麦粉の量を $2700~{\rm g}$ 以内, キャベツの量を $1500~{\rm g}$ 以内として売上をできるだけ多くするには, 広島風のお好み焼きと関西風のお好み焼きをどのように作ればよいか。
また, この時の売上の最大値を求めなさい。ただし, 作ったお好み焼きは全て売れるものとする。
広島風のお好み焼きを $x$ 枚, 関西風のお好み焼きを $y$ 枚作るとします。
この時, 使用する小麦粉の量は $400x + 100y~{\rm [g]}$, キャベツの量は $100x + 300y ~{\rm [g]}$ になります。
よって与えられた条件を表す領域を図示すると, その領域は連立不等式
$\begin{cases} x\geqq 0 \\ y \geqq 0 \\ 400x + 100y \leqq 2700\\ 100x + 300y \leqq 1500 \end{cases}$
の表す領域と等しくなります。
売上を $k$ [円] とすると $k = 400x + 500y$ であり, 式を書き直すと
$400x + 500y -k=0$
この直線が上で定めた領域と共有点を持つような $k$ の値の最大値を求めればよいことになります。
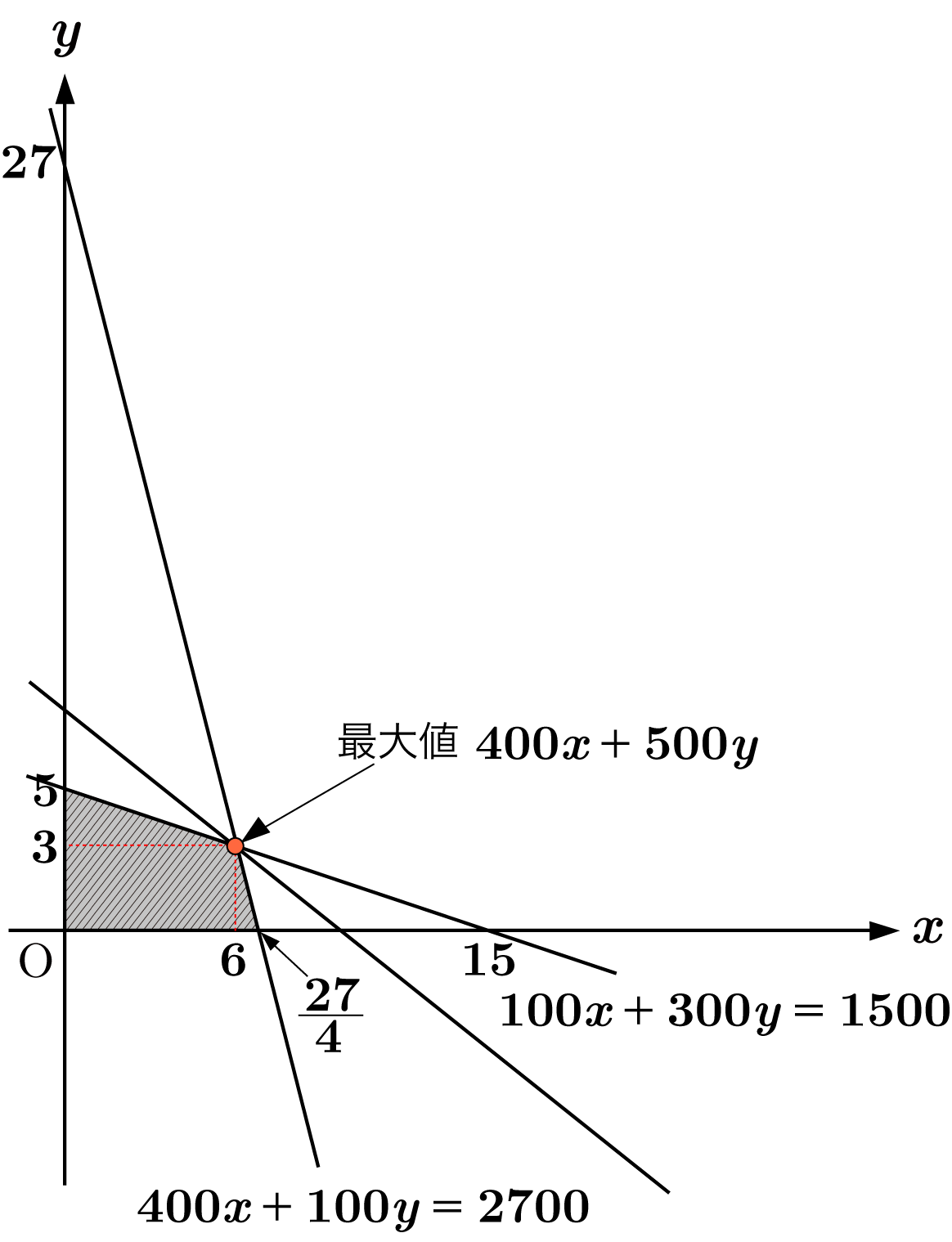
上図からこの直線は点 $(6,3)$ を通る時, $k$ の値が最大となるので, $x=6$, $y=3$ の時 $k$ は最大値 $3900$ を取ることがわかります。
よって, 広島風のお好み焼きを $6$ 枚, 関西風のお好み焼きを $3$ 枚作った時に売上は最大となり, その時の売上は $3900$ 円となります。

ショートケーキを $100x$ 個, フルーツケーキを $100y$ 個作るとします。
この時, 必要な卵の数は $2x + y~{\rm [kg]}$, 必要な砂糖の数は $x + 2y~{\rm [kg]}$ になります。
よって与えられた条件を表す領域を $xy$ 平面に図示すると, その領域は連立不等式
$\begin{cases} x \geqq 0 \\ y \geqq 0 \\ 2x+y \leqq 9 \\ x+2y \leqq 9 \end{cases}$
の表す領域と等しくなります。
売上を $k$ [万円] とすると $k = 5x + 7y$ であり, 式を書き直すと
$5x + 7y -k =0$
この直線が上で定めた領域と共有点を持つような $k$ の値の最大値を求めればよいことになります。
上図から, この直線は点 $(3,3)$ を通る時 $k$ の値が最大となるので, $x = 3$, $y=3$ の時, $k$ は最大値 $36$ を取ることがわかります。
よってショートケーキを $300$ 個, フルーツケーキを $300$ 個作った時に売り上げは最大となり, その金額は $36$ 万円になります。