$Q1$.
正方形 ${\rm ABCD}$ の頂点を始点と終点に持つベクトルを考える。
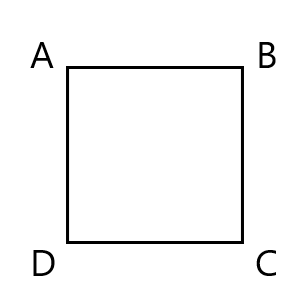
この時, 以下の問いに答えなさい。
$Q2$.
下図のような正六角形 ${\rm ABCDEF}$ の頂点か点 ${\rm O}$ のいずれかを始点と終点に持つベクトルを考える。
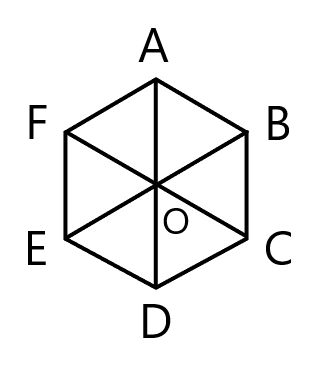
この時, 以下の問いに答えなさい。
(1)
${\rm ABCDEF}$ が正六角形であることから線分 ${\rm FC}$, ${\rm ED}$ はそれぞれ線分 ${\rm AB}$ と平行になります。
また, ${\rm FC} = 2 {\rm AB}$ であり ${\rm O}$ は線分 ${\rm FC}$ の中点となるので
${\rm AB} = {\rm FO} = {\rm OC} = {\rm ED}$
となります。
(2)
まず $-\overrightarrow{{\rm OE}} = \overrightarrow{{\rm EO}}$ なので $\overrightarrow{{\rm EO}}$ が $\overrightarrow{{\rm OE}}$ の逆ベクトルであることがわかります。
また (1) と同様に考えれば
$\overrightarrow{{\rm EO}} = \overrightarrow{{\rm FA}} = \overrightarrow{{\rm OB}} = \overrightarrow{{\rm DC}}$
であることがわかるので, これらが $\overrightarrow{{\rm OE}}$ の逆ベクトルになります。
(3)
${\rm AB} = 1$ の時
${\rm AO} = {\rm OD} = 1$
となるので線分 ${\rm AD}$ の大きさは $1+1=2$ となります。

(1)
その「長さ」と「向き」が一致する時, $2$ つのベクトルは等しいといいます。
${\rm ABCD}$ は正方形であることから ${\rm AB} = {\rm DC}$ かつ, 線分 ${\rm AB}$ と ${\rm DC}$ は平行となるので, $\overrightarrow{{\rm DC}}$ と $\overrightarrow{{\rm AB}}$ は等しくなります。
$\overrightarrow{{\rm CD}}$ は向きが反対なので等しいベクトルとは言わないことに注意しましょう。
また, 解答では省略しましたが, $\overrightarrow{{\rm AB}}$ 自身も当然 $\overrightarrow{{\rm AB}}$ と等しいベクトルです。
(2)
あるベクトルと「長さ」が同じで「向き」が反対のベクトルを, そのベクトルの逆ベクトルといいます。
$\overrightarrow{{\rm DA}}$ と長さが等しく向きが反対のベクトルは $\overrightarrow{{\rm AD}}$ と $\overrightarrow{{\rm BC}}$ の $2$ つになります。
$\overrightarrow{{\rm AD}} = -\overrightarrow{{\rm DA}}$ のように, 始点と終点を入れ換えたベクトルは逆ベクトルになることに注意しましょう。
(3)
始点と終点が一致するようなベクトルを零ベクトルといいます。
ここでは頂点が $4$ つあるので, $4$ つの零ベクトルを考えることができます。