$n$ 個の頂点を持つ無向グラフに対し, 頂点 $i$ と頂点 $j$ の間に辺がある時 $(i,j)$ 成分と $(j,i)$ 成分が $1$ であり, それ以外の成分が $0$ であるような $n$ 次正方行列をそのグラフの隣接行列という。
次の無向グラフの隣接行列として最も適切なものを以下の選択肢から選びなさい。
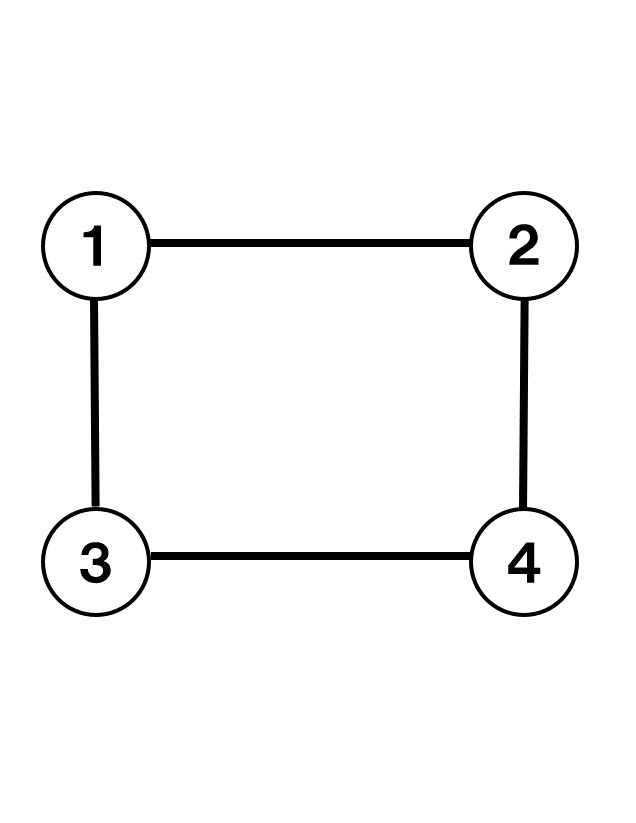
$\begin{pmatrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 \end{pmatrix}$
$\begin{pmatrix} 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \end{pmatrix}$
$\begin{pmatrix} 1 & 1 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 1 \end{pmatrix}$
$\begin{pmatrix} 1 & 1 & 1 & 1 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 \end{pmatrix}$
頂点 $1$ と $2$ の間, $1$ と $3$ の間, $2$ と $4$ の間, $3$ と $4$ の間にそれぞれ辺があるので, $(1,2)$ 成分, $(2,1)$ 成分, $(1,3)$ 成分, $(3,1)$ 成分, $(2,4)$ 成分, $(4,2)$ 成分, $(3,4)$ 成分, $(4,3)$ 成分が $1$ で, それ以外の成分を $0$ にすればよい。
よって隣接行列は $\begin{pmatrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 \end{pmatrix}$ となる。
