3
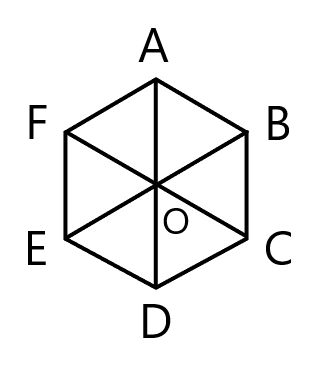
正六角形 ${\rm ABCDEF}$ において, $\overrightarrow{{\rm AE}} + \overrightarrow{{\rm DB}}$ と等しいベクトルを以下の選択肢から選びなさい。
$\overrightarrow{{\rm OO}}$
$\overrightarrow{{\rm AF}}$
$\overrightarrow{{\rm DA}}$
$\overrightarrow{{\rm BA}}$
$\overrightarrow{{\rm DB}} = \overrightarrow{{\rm EA}}$ であるから
$→AE+→DB=→AE+→EA=→AA$
よって $\overrightarrow{{\rm AE}} + \overrightarrow{{\rm DB}}$ は零ベクトルであるので $\overrightarrow{{\rm AE}} + \overrightarrow{{\rm DB}} = \overrightarrow{{\rm OO}}$ である。
一般に, 逆ベクトルとの和は零ベクトルになることに注意する。
$\overrightarrow{a} + (-\overrightarrow{a}) = (-\overrightarrow{a}) + \overrightarrow{a} = \overrightarrow{0}$
