ベクトルの和 02 | アドウィンテクノ塾

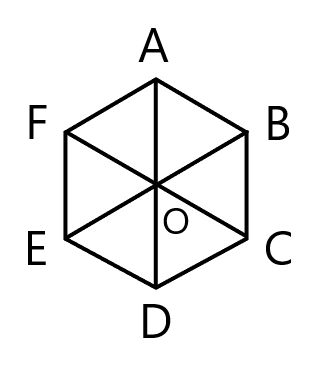
正六角形 ${\rm ABCDEF}$ において, $\overrightarrow{{\rm AC}} + \overrightarrow{{\rm BO}}$ と等しいベクトルを以下の選択肢から選びなさい。

正六角形

$\overrightarrow{{\rm AD}}$

$\overrightarrow{{\rm OD}}$

$\overrightarrow{{\rm AE}}$

$\overrightarrow{{\rm FC}}$

$\overrightarrow{{\rm BO}} = \overrightarrow{{\rm CD}}$ であるから

$\begin{eqnarray*} \overrightarrow{{\rm AC}} + \overrightarrow{{\rm BO}} & = & \overrightarrow{{\rm AC}} + \overrightarrow{{\rm CD}}\\ & = & \overrightarrow{{\rm AD}}\end{eqnarray*}$

よって $\overrightarrow{{\rm AC}} + \overrightarrow{{\rm BO}} = \overrightarrow{{\rm AD}}$ である。