$Q1$.
次の微分方程式の階数を答えなさい。
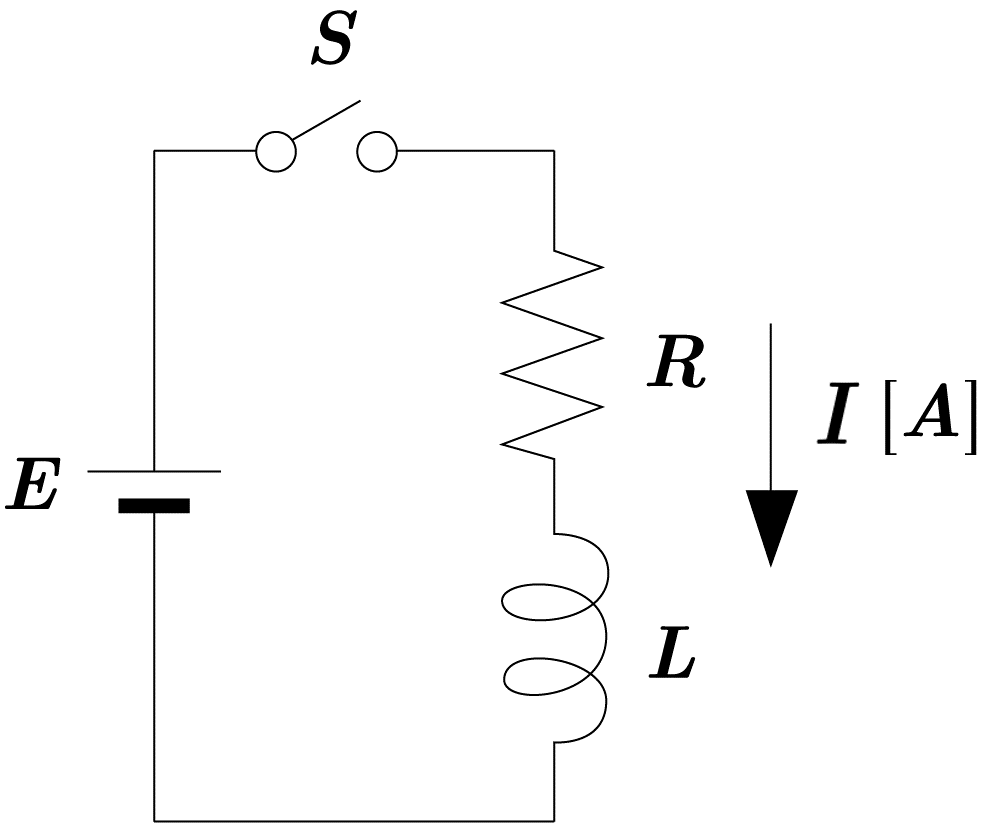
$Q2$.
右図の $RL$ 直列回路においてスイッチを ${\rm ON}$ にした時, 時刻 $t$ における電流を $I(t)[A]$ とすると次の式が成り立つ。
この時, 次の問いに答えなさい。
微分方程式が与えられた時, その関係式を成り立たせるような関数をその微分方程式の解と言います。
(1)
微分方程式の解で, 任意定数を含むようなものをその微分方程式の 一般解 といいます。
$I = \dfrac{E}{R} + Ce^{-\frac{R}{L}t }$ とすると
$\dfrac{dI}{dt} = -\dfrac{CR}{L}e^{-\frac{R}{L}t}$
であるから
$\begin{eqnarray*}RI+L\dfrac{dI}{dt} & = & \left(E+CRe^{-\frac{R}{L}t}\right) + L\left( -\dfrac{CR}{L}e^{-\frac{R}{L}t} \right)\\[1em] & = & E + CRe^{-\frac{R}{L}t} - CRe^{-\frac{R}{L}t} = E \end{eqnarray*}$
よって $RI + L \dfrac{dI}{dt} = E$ が成り立つことがわかります。
$I$ はこの微分方程式を満たし任意定数を含むので, この微分方程式の一般解になります。
(2)
$I = \dfrac{E}{R} + Ce^{-\frac{R}{L}t }$ とし $I(0)=0$ とすると
$\dfrac{E}{R} + C = 0$
$C = -\dfrac{E}{R}$ なので, この時の特殊解は
$I = \dfrac{E}{R} - \dfrac{E}{R}e^{-\frac{R}{L}t} = \dfrac{E}{R}\left(1- e^{-\frac{R}{L}t} \right)$
となります。
$Q3$.
$C_1,~C_2$ を任意定数として, 関数 $y = C_1e^{2x} + C_2e^{-x}$ を一般解とするような微分方程式を求めなさい。
与えられた関数とその導関数を使って $2$ つの任意定数を消去することを考えます。
$y = C_1e^{2x} + C_2e^{-x}$ として, 微分すると
$\dfrac{dy}{dx} = 2C_1e^{2x}- C_2e^{-x}$
$\dfrac{d^2y}{dx^2} = 4C_1e^{2x}+ C_2e^{-x}$
よって
$y + \dfrac{dy}{dx} = 3C_1e^{2x}$
$\dfrac{dy}{dx} + \dfrac{d^2y}{dx^2} = 6C_1e^{2x}$
この $2$ 式から $C_1$ を消去すると
$\left( \dfrac{dy}{dx} + \dfrac{d^2y}{dx^2} \right) - 2\left( y + \dfrac{dy}{dx} \right) = 0$
左辺を整理すれば $\dfrac{d^2y}{dx^2} - \dfrac{dy}{dx} = 2y=0$ となります。

関数とその導関数を含む関係式を微分方程式といい, 関係式に含まれる導関数の最高次数をその微分方程式の 階数 といいます。
(1)
未知関数 $x$ と $x$ の導関数を含む関係式なので, これは $x$ に関する $1$ 階微分方程式です。
(2)
未知関数 $x$ と $x$ の第 $2$ 次導関数を含む関係式なので, これは $x$ に関する $2$ 階微分方程式です。
(3)
未知関数 $y$ と $y$ の導関数と第 $2$ 次導関数を含む関係式なので, これは $y$ に関する $2$ 階微分方程式です。
(4)
未知関数 $T$ と $T$ の導関数を含む関係式なので, これは $T$ に関する $1$ 階微分方程式です。
$\left( \dfrac{dT}{dx} \right)^2$ は $T$ の第 $2$ 次導関数ではなく $T$ の導関数の $2$ 乗です。