$Q1$.
$A = \{ x~|~x$ は $100$ 以下の素数 $\}$ とした時, 次の整数が $A$ に属するかどうか答えなさい。
$Q2$.
次の集合の部分集合を全て求めなさい。
空集合 $\emptyset$ も部分集合であることを忘れないようにしましょう。
一般に, 要素の数が $n$ である有限集合に対し, その部分集合は $2^n$ 個存在します。
要素の数が少ないものから数えることで数え忘れることの無いようにしましょう。
$Q3$.
$U = \{ 0,1,2,3,4,5,6,7,8,9,10 \}$
を全体集合とし, $A,B \subset U$ を
$A = \{1,3,6,7\}$, $B=\{1,2,3,4,7\}$
と定める。この時, 次の集合を求めなさい。
(1)
$A$ と $B$ の両方に属するものの集合を, $A$ と $B$ の共通部分といいます。
$A$ と $B$ のどちらにも属している数は $1,3,7$ なので $A \cap B = \{ 1,3,7\}$ となります。
(2)
$A$ と $B$ の少なくとも一方に属するものの集合を, $A$ と $B$ の和集合といいます。
$A$ と $B$ の少なくとも一方に属している数は $1,2,3,4,6,7$ なので $A \cup B = \{ 1,2,3,4,6,7\}$ となります。
(3)
全体集合 $U$ の要素で, $B$ に属さないものの集合を $B$ の補集合といいます。
$U$ の要素で $B$ に属さない数は $0,5,6,8,9,10$ なので $\overline{B} = \{ 0,5,6,8,9,10\}$ となります。
よって $A$ と $\overline{B}$ の共通部分は $A \cap \overline{B} = \{6\}$ となります。
(4)
ド・モルガンの法則から
$\overline{A} \cup \overline{B} = \overline{A \cap B}$
が成り立ちます。(1) より $A \cap B = \{ 1,3,7\}$ なので, その補集合は
$\overline{A \cap B} = \{0,2,4,5.6,8,9,10\}$
となります。
$Q4$.
$1$ 以上 $100$ 以下の整数のうち, 以下を満たす数の個数を求めなさい。
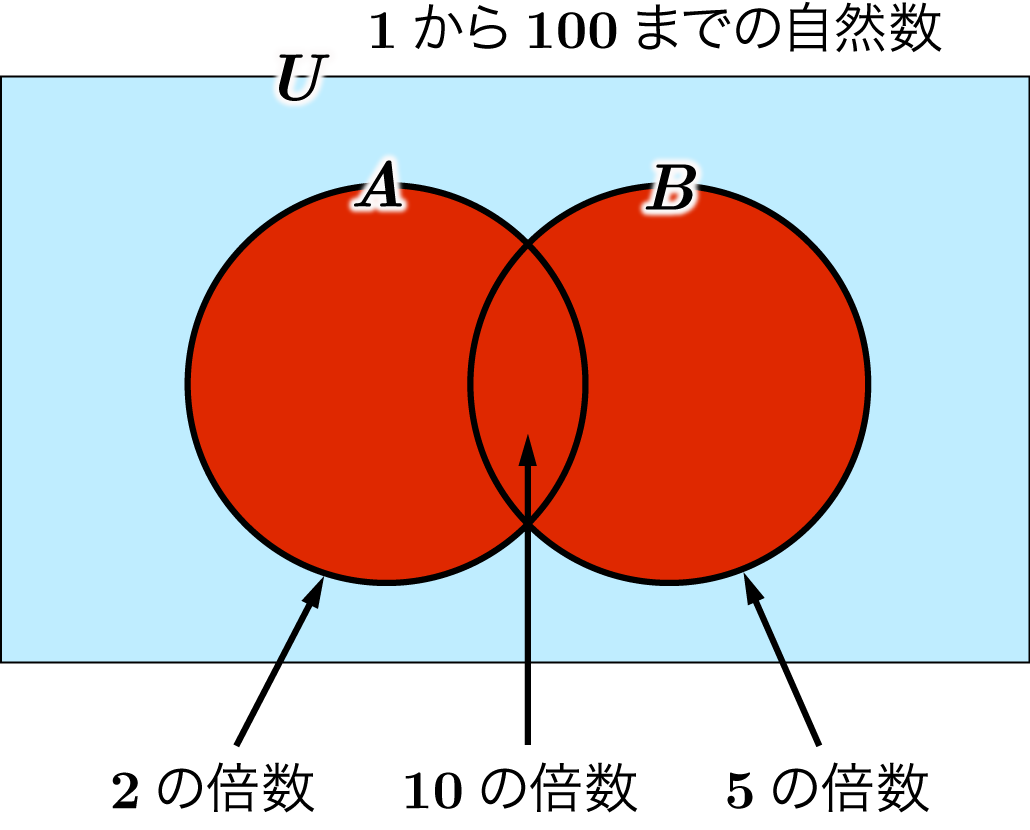
$U = \{x~|~x$ は $1$ 以上 $100$ 以下の整数 $\}$
を全体集合とし, 部分集合 $A$, $B \subset U$ を
と定めます。
(1)
$2$ でも $5$ でも割り切れる数は $10$ の倍数です。$1$ 以上 $100$ 以下の $10$ の倍数は
$10,20,30,40,50,60,70,80,90,100$
の $10$ 個となります。
[別解]
整数 $k$ に対し, $1 \leqq 10k \leqq 100$ とすると $1\leqq k \leqq 10$ であることがわかります。
この不等式を満たす整数 $k$ の数は $10$ 個なので, $100$ 以下の $10$ の倍数は $10$ 個あることがわかります。
(2)
$2$ で割り切れるか $5$ で割り切れる数の集合は $A \cup B$ と表せるので, $A \cup B$ の要素の数を求めればよいことになります。
(1) と同様に考えると $A$ の要素の数は $50$ 個, $B$ の要素の数は $20$ 個であることがわかります。ここで
($A$ の要素の数) $+$ ($B$ の要素の数)
を考えると, $A \cap B$ の要素は $2$ 回数えられることになるので
($A \cup B$ の要素の数) $=$ ($A$ の要素の数) $+$ ($B$ の要素の数) $-$ ($A \cap B$ の要素の数)
が成り立ちます。
(1) より $A \cap B$ の要素の数は $10$ 個なので
($A \cup B$ の要素の数) $= 50 + 20 - 10 = 60$
よって $1$ 以上 $100$ 以下の整数で, $2$ で割り切れるか $5$ で割り切れるものは $60$ 個あることがわかります。
(3)
$2$ でも $5$ でも割り切れない数の集合は $\overline{A} \cap \overline{B}$ と表せます。ド・モルガンの法則から
$\overline{A} \cap \overline{B} = \overline{A \cup B}$
であり, ここで $A \cup B$ の補集合とは $U$ の要素で $A \cup B$ に属さないものの集合なので
($\overline{A \cup B}$ の要素の数) $=$ ($U$ の要素の数) $-$ ($A \cup B$ の要素の数)
が成り立ちます。 (2) から $A \cup B$ の要素の数は $60$ 個であり, $U$ の要素の数は $100$ 個なので
$\overline{A \cup B}$ の要素の数は $100 - 60 =40$ 個になります。

素数とは $2$ 以上の整数で, $1$ と自分自身以外の約数を持たない数のことです。
(1)
$2 \lt 100$ であり, $2$ は素数なので, $2$ は $A$ に属します。
(2)
$33 = 3\cdot 11$ より, $33$ は素数ではありません。よって $33$ は $A$ に属しません。
(3)
$89$ は $1$ と $89$ 以外に約数を持ちません。$89 \lt 100$ なので $33$ は $A$ に属します。
(4)
$103$ は素数ですが $100$ より大きい数です。よって $103$ は $A$ に属しません。
(5)
負の数は素数ではないので, $-5$ は素数ではありません。よって $-5$ は $A$ に属しません。