$\overrightarrow{0}$ でない $2$ つの平面ベクトルが平行でない時, それらのベクトルは線形独立であるといいます。

逆に $2$ つの平面ベクトルが平行である時は線形従属であるといいます。

$\overrightarrow{0}$ でない $2$ つのベクトル $\overrightarrow{a}$ と $\overrightarrow{b}$ が平行である時 $\overrightarrow{b} = k\overrightarrow{a}$ と表せることに注意しましょう。

(1)

$(-1,-1) = (-1)(1,1)$

より, これらのベクトルは平行なので線形従属です。

(2)

$(-5,4) = k(4,-5)$

とすると, $x$ 成分から $4k = -5$ より $k = -\dfrac{5}{4}$ となります。

一方 $y$ 成分から $-5k = 4$ より $k = -\dfrac{4}{5}$ となります。

すなわち, これらを同時に満たす $k$ は存在しないので, $2$ つのベクトルは平行ではありません。

よってこれらのベクトルは線形独立です。

(3)

$(-2,1) = k(4,2)$

とすると, (2) と同様に考えれば $k=-\dfrac{1}{2}$ かつ $k= \dfrac{1}{2}$ となり, このような $k$ は存在しません。

よってこれらのベクトルは線形独立になります。

(4)

$(2,4) = \dfrac{1}{3}(6,12)$

より, これらのベクトルは平行なので線形従属です。

まず $\overrightarrow{e_1} = s\overrightarrow{x} + t\overrightarrow{y}$ とすると

$\begin{cases} s - t = 1 \\ s + t = 0 \end{cases}$

この連立方程式を解くと $s = \dfrac{1}{2}$, $t = -\dfrac{1}{2}$ となります。

よって $\overrightarrow{e_1} = \dfrac{1}{2}\overrightarrow{x} - \dfrac{1}{2}\overrightarrow{y}$ となります。

また $\overrightarrow{e_2} = s\overrightarrow{x} + t\overrightarrow{y}$ とすると

$\begin{cases} s-t = 0 \\s +t=1 \end{cases}$

この連立方程式を解くと $s = t = \dfrac{1}{2}$ となります。

よって $\overrightarrow{e_2} = \dfrac{1}{2}\overrightarrow{x} + \dfrac{1}{2}\overrightarrow{y}$ となります。

$\overrightarrow{{\rm AB}} = \overrightarrow{b}$, $\overrightarrow{{\rm AC}} = \overrightarrow{c}$ とします。

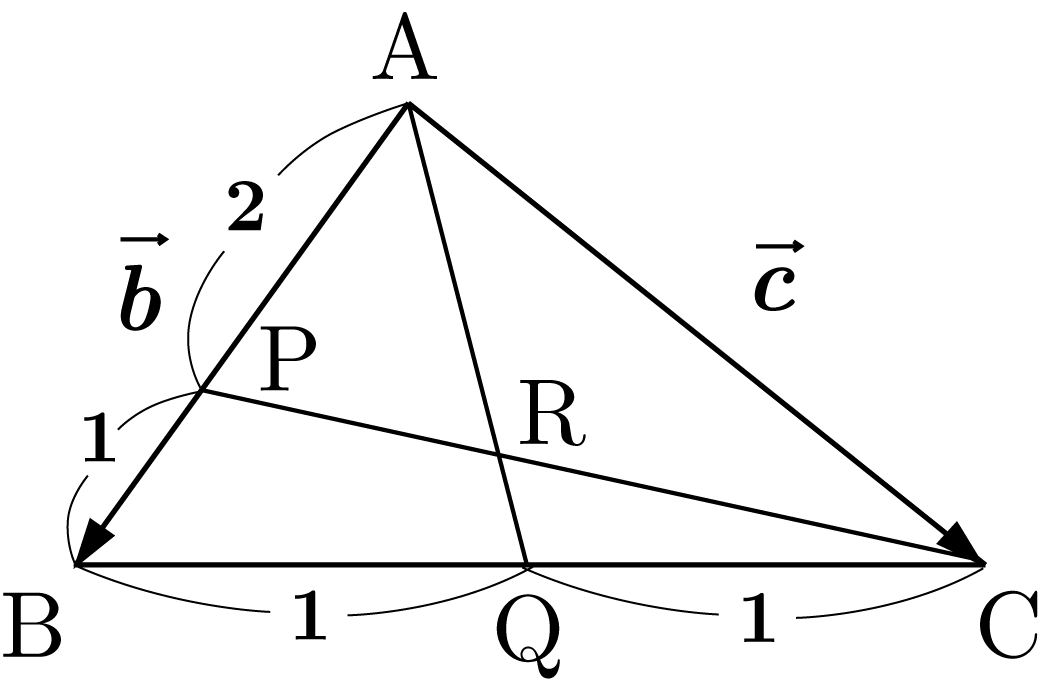
すると点 ${\rm P}$ は線分 ${\rm AB}$ を $2:1$ に内分するので

$\overrightarrow{{\rm AP}} = \dfrac{2}{3} \overrightarrow{b} ~ \cdots(1)$

また, 点 ${\rm Q}$ は 線分 ${\rm BC}$ の中点であるから

$\overrightarrow{{\rm AQ}} = \dfrac{ \overrightarrow{b} + \overrightarrow{c}}{2}~ \cdots(2)$

が成り立ちます。

${\rm PR:RC} = m:n$ とすると, 点 ${\rm R}$ は線分 ${\rm PC}$ を $m:n$ に内分する点なので

$\overrightarrow{{\rm AR}} = \dfrac{n \overrightarrow{{\rm AP}} + m\overrightarrow{{\rm AC}} }{m+n} ~ \cdots(3)$

ここで ${\rm R}$ は線分 ${\rm AQ}$ 上にあるので, 実数 $k$ を用いて

$\overrightarrow{{\rm AR}} = k \overrightarrow{{\rm AQ}}$

と表せます。$(3)$ より

$\dfrac{n \overrightarrow{{\rm AP}} + m\overrightarrow{{\rm AC}} }{m+n} = k \overrightarrow{{\rm AQ}}$

$(1)$, $(2)$ をそれぞれ代入すると

$\dfrac{1}{m+n} \left( \dfrac{2n}{3}\overrightarrow{b} + m\overrightarrow{c} \right) = \dfrac{k}{2}\left( \overrightarrow{b} + \overrightarrow{c} \right)$

$\overrightarrow{b}$ と $\overrightarrow{c}$ を左辺にまとめて整理すると

$\left( \dfrac{2n}{3(m+n)} - \dfrac{k}{2} \right) \overrightarrow{b} + \left( \dfrac{m}{m+n} - \dfrac{k}{2} \right) \overrightarrow{c} = \overrightarrow{0}$

すると $\overrightarrow{b}$ と $\overrightarrow{c}$ は線形独立なので

$\begin{eqnarray*} \dfrac{2n}{3(m+n)} - \dfrac{k}{2} & = & 0 \\[1em] \dfrac{m}{m+n} - \dfrac{k}{2} & = & 0 \end{eqnarray*}$

が成り立ちます。$2$ つの式から $k$ を消去すると

$\dfrac{2n}{3(m+n)} = \dfrac{m}{m+n}$

両辺に $m+n$ をかければ $m = \dfrac{2}{3}n$ となるので

$m:n = \dfrac{2}{3}n:n = 2:3$

となります。